Основные законы магнитного поля
Теорема Гаусса для поля 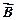
Поток вектора 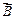 сквозь любую замкнутую поверхность равен нулю:
сквозь любую замкнутую поверхность равен нулю:
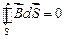 .
.
Эта теорема выражает собой в постулативной форме тот экспериментальный факт, что линии вектора 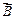 не имеют ни начала, ни конца. Поэтому число линий вектора
не имеют ни начала, ни конца. Поэтому число линий вектора 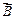 , выходящих из любого объема, ограниченного замкнутой поверхностью
, выходящих из любого объема, ограниченного замкнутой поверхностью  , всегда равно числу линий, входящих в этот объем.
, всегда равно числу линий, входящих в этот объем.
Отсюда вытекает важное следствие: поток вектора 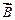 сквозь поверхность
сквозь поверхность 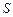 , ограниченную некоторым замкнутым контуром, не зависит от формы поверхности
, ограниченную некоторым замкнутым контуром, не зависит от формы поверхности 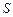 .
.
Циркуляция вектора 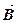
Циркуляцией вектора 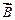 по заданному замкнутому контуру называется интеграл
по заданному замкнутому контуру называется интеграл
 ,
,
где 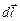 – вектор элементарной длины контура, направленный вдоль обхода контура;
– вектор элементарной длины контура, направленный вдоль обхода контура; 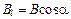 – составляющая вектора
– составляющая вектора 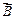 в направлении касательной к контуру (с учетом выбранного направления обхода);
в направлении касательной к контуру (с учетом выбранного направления обхода); 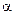 – угол между векторами
– угол между векторами 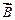 и
и 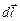 .
.
Теорема о циркуляции вектора 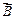 : циркуляция вектора
: циркуляция вектора 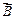 по произвольному замкнутому контуру равна произведению магнитной постоянной
по произвольному замкнутому контуру равна произведению магнитной постоянной 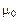 на алгебраическую сумму токов, охватываемых этим контуром:
на алгебраическую сумму токов, охватываемых этим контуром:
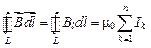 (1.12)
(1.12)
 где
где 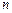 – число проводников с токами, охватываемых контуром
– число проводников с токами, охватываемых контуром 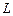 произвольной формы.
произвольной формы.
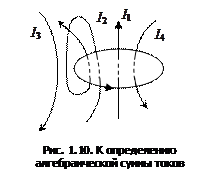
Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рис. 1.10.
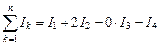 .
.
Теорема о циркуляции вектора 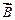 имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био–Савара–Лапласа.
имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био–Савара–Лапласа.
1.13. Применение теоремы о циркуляции вектора 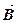
Дата добавления: 2015-09-18; просмотров: 765;
