Частично-рекурсивные функции
Функция f(x1, . . . , xn+1) получается из функции g(x1, . . . , xn+1) с помощью операции минимизации, если справедливо следующее соотношение:
f(x1, ... , xn+1) = mt(g(x1, . . . , xn, t) = xn+1) (1)
Приведенная запись означает, что должны выполняться следующие два свойства:
1) f(x1, . . . , xn+1) равно наименьшему t, при котором выполняется равенство в правой части соотношения (1);
2) все значения g(x1, ... , xn, i), i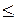 
t определены.
Нетрудно проверить, что если функция g является вычислимой, то функция f, получаемая из g с помощью операции минимизации, также оказывается вычислимой.
Действительно, для того, чтобы найти значение f(x1, . . . , xn+1), достаточно последовательно определять значения g(x1, . . . , xn, 0), . . . , g(x1, . . . , xn, i), . . . , до тех пор, пока в такой последовательности значений впервые не встретится значение, равное xn+1. При этом каждое следующее значение получаемой последовательности не вычисляется до тех пор, пока не вычислено предыдущее значение.
Тогда первое значение i, для которого g(x1, . . . , xn, i) = xn+1, берется в качестве f(x1, . . . , xn+1).
Пример. Если g(x, y) = x+y, то f(x, y) = mt(g(x, t) = y) - это следующая функция:
f(x, y) =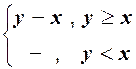 
.
Приведенный пример показывает, что функция f, получаемая из функции g с помощью операции минимизации, может оказаться не всюду определенной, или частичной вычислимой, функцией.
Упражнение. Показать, что если числовая функция f(x) имеет обратную функцию, то f-1(x) = mt(f(t) = x).
Дата добавления: 2015-09-18; просмотров: 480;