I I I S
1 1 1
<3><3>1 1 1 1 1 1 1 1<2> 1
Рис. 8.1
Здесь записи <2> и <3>использованы для представления чисел 2 и 3 в унарной системе счисления.
Упражнение. Построить дерево, представляющее функцию умножения p(x1, x2) = x1 ´ x2.
Возьмем алфавит A= {I, S, O, P, C, M, 1, $}, состоящий из специального символа$ и символов, c помощью которых осуществлялась разметка вершин деревьев, представляющих частично-рекурсивные функции.
Символ$ будем называть разделителем.
Если D - дерево, представляющее определение некоторой частично - рекурсивной функции, то осуществим левосторонний обход D сверху вниз, выписывая слова в алфавите A, приписанные вершинам дерева в порядке их прохождения. При этом выписываемые слова разделяются символом $.
Полученное в результате слово 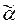 D назовем кодом дерева D.
D назовем кодом дерева D.
Например, дерево, представляющее функцию f(x1, x2) = x1+x2, которое приведено ранее, имеет код:
P$I$1$1$1$C$I$<3>$<3>$1$1$1$I$1$1$1$I$1$1$2$S$1.
Из правил построения деревьев, представляющих частично-рекурсивные функции, следует, что по произвольной вершине и ее левому поддереву однозначно определяется число потомков этой вершины.
Действительно, всякая внутренняя вершина дерева помечена одним из символов операций или функций. Если это символы O, S, P или M, то число потомков такой вершины заранее известно.
Если же внутренняя вершина дерева помечена символом C, то число потомков этой вершины определяется числом переменных функции, дерево представления которой имеет корнем самого левого потомка исходной вершины. Если же корень дерева помечен символом I, то число потомков этой вершины равно n + 2, где n – число, унарная запись которого размечает вершину левого потомка корня дерева.
Следовательно, степень всякой внутренней вершины, помеченной символом C,становится известна, как только полностью пройдено левое поддерево этой вершины и оказывается определенным число переменных функции, представляемой этим поддеревом.
Вершина дерева является висячей, если она помечена числом в унарной системе.
Поэтому, если задан код 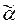 D некоторого дерева, то само дерево по своему коду может быть восстановлено с помощью подходящей процедуры.
D некоторого дерева, то само дерево по своему коду может быть восстановлено с помощью подходящей процедуры.
Рассмотрим последовательность всех слов в алфавите A, выписанных в порядке возрастания их длин, а слов одинаковой длины в лексикографическом порядке.
Из этой последовательности выделим подпоследовательность слов:
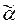 D1, D1, 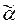 D2, . . . , D2, . . . , 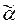 Di, . . . , Di, . . . ,
| (1) |
являющихся кодами деревьев.
Нетрудно заметить, что существует эффективная процедура, позволяющая по произвольному числу k найти слово 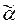 Dk в этой последовательности.
Dk в этой последовательности.
Последовательности (1) соответствует последовательность (2), состоящая из частично-рекурсивных функций, представляемых деревьями, имеющими коды последовательности (1).
| g1, g2, . . . , gi, . . . | (2) |
Обозначим как Dgi - дерево, представляющее функцию gi.
Существует эффективная процедура, которая по всякому числу n строит определение частично рекурсивной функции gn.
Следовательно, зная порядковый номер n частично рекурсивной функции gn в последовательности (2), можно эффективно найти рекурсивную схему определения этой функции. То есть по номеру функции в последовательности (2) может быть восстановлено описание метода вычисления значений этой функции.
Отметим простейшие свойства последовательности (2):
-всякая частично рекурсивная функция встречается в (2) бесконечное число раз;
- последовательность (2) содержит счетно-бесконечное множество различных функций;
- существуют числовые функции, не содержащиеся в (2).
По последовательности (2) определим последовательность (3), содержащую все одноместные частично-рекурсивные функции.
| f1, f2, . . . , fi, . . . | (3) |
Здесь функция fi задается деревом, полученным из дерева Dgi, отождествлением всех переменных, т.е. функция fi получается из функции gi отождествлением переменных.
Введем обозначения F - для множества всех частично-рекурсивных функций и F1- для множества всех одноместных частично-рекурсивных функций.
Отображение n, которое всякому числу n ставит в соответствие функцию fn, назовем нумерацией множества F1.
При этом индекс n функции fn назовём n номером этой функции в нумерации n: N ® F1.
Отображение p: N ® F, которое всякому числу n ставит в соответствие функцию gn, назовем нумерацией множества F.
Заметим, что обе нумерации n и p являются вычислимыми, поскольку существуют эффективные процедуры, которые для каждого значения целого неотрицательного числа n строят рекурсивные определения соответствующих функций.
Дата добавления: 2015-09-18; просмотров: 572;
