ФУНКЦИЙ
Ниже будет построена специальная последовательность, состоящая из всех частично-рекурсивных функций.
Для этого полное определение произвольной частично- рекурсивной функции представляется в виде специального нагруженного дерева.
Все такие деревья нумеруются с помощью неотрицательных целых чисел, а представляемые ими частично-рекурсивные функции образуют последовательность всех таких функций, в которую они входят в порядке возрастания номеров соответствующих деревьев.
Будем считать, что для обозначения переменных функций используются только следующие символы: x1, . . . , xi, . . .
При разметке вершин деревьев используются следующие символы:
1)C, P, M -для обозначения операций суперпозиции, примитивной рекурсии и минимизации;
2) 1-для записи индексов переменных в унарной системе;
3) I, S, O - для обозначения простейших функций.
Определим деревья, представляющие схемы определения частично-рекурсивных функций, с помощью следующих правил:
1. Функции O(xi), S(xi) и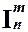 
(xi1, ... , xin) представляются следующими деревьями:
O S I
iim n i1 . . . in
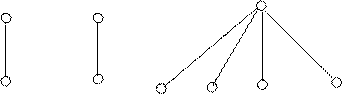
2. Если h(xj1, . . . , xjr) =
= f(g1(x1,1, . . . , x1,m1), . . . , gk(xk,1, . . . , xk,mk)), то она представляется деревом:
C
D f Dg1 . . . Dgk
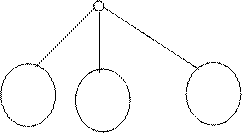
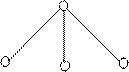Здесь Df, Dg1, ... , Dgk - это деревья, представляющие функции, входящие в суперпозицию. В частности, если gi = xj, то есть представляет собой переменную, то соответствующее дерево имеет вид:
I
1 1 j
3. Пусть f(x1, . . . , xn+1) получается из g(x1, . . . , xn) и h(x1, . . . , xn, xn+1, xn+2) с помощью операции примитивной рекурсии:
f(x1, . . . , xn, 0) = g(x1, . . . , xn);
f(x1, . . . , xn, y+1) = h(x1, . . . , xn, y, f(x1, . . . , xn, y)).
Тогда f представляется деревом:
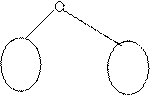P
Dg Dh
4. Если f(x1, . . . , xn+1) = m t(g(x1, . . . , xn, t) = xn+1), то дерево, представляющее f, имеет вид:
M
Dg
Пример.Построим дерево, представляющее функцию f(x1, x2) = x1+ x2.
Эта функция была определена ранее с помощью следующей схемы примитивной рекурсии:
f(x1, 0) =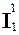 
(x1);
f(x1, x2 + 1)=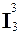 
(x1, x2, S(f(x1, x2)).
Здесь определения функций g и h, из схемы примитивной рекурсии, даны в полном виде с указанием всех переменных (в том числе и несущественных) этих функций в определении схемы примитивной рекурсии.
Поэтому дерево определения f имеет вид, приведенный на рис. 8.1:
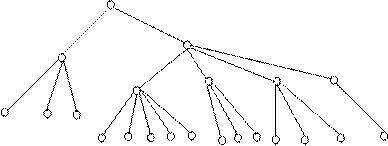P
I C
Дата добавления: 2015-09-18; просмотров: 516;