ОПРЕДЕЛЕНИЕ
Функции, получаемые из простейших функций с помощью конечного числа применений операций суперпозиции и примитивной рекурсии, называются примитивно-рекурсивными.
Из приведенного определения следует, что всякая примитивно-рекурсивная функция является всюду определенной функцией. Кроме того, все примитивно-рекурсивные функции вычислимы.
Упражнение. Показать, что если f(x1, x2) является примитивно-рекурсивной функцией, если она выражается через примитивно-рекурсивные функции g и h с помощью соотношений
f(0, x) = g(x); (1)
f(y+1, x) = h(x, y, f(y, x)). (2)
Доказательство справедливости приведенного в упражнении утверждения обосновывать примитивную рекурсивность функций, определяемых рекурсивными схемами, в которых рекурсия ведется по произвольной переменной.
Рассмотрим примеры примитивно-рекурсивных функций.
1. Сумма f(x, у) = x + у задается следующей схемой примитивной рекурсии:
f(x, 0) = 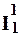 (x);
(x);
f(x, у+1) = S(f(x, у)).
То есть f(x ,у) получается из элементарных функций g(x1)= 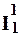 (x1) и h(x1, x2, x3) =S(
(x1) и h(x1, x2, x3) =S(  ( x1, x2, x3)) с помощью операции примитивной рекурсии и поэтому является примитивно-рекурсивной.
( x1, x2, x3)) с помощью операции примитивной рекурсии и поэтому является примитивно-рекурсивной.
2. Произведение p(x, у) = x ´ у задается схемами:
p(x, 0) = O(x);
p(x, у+1) = x+ p(x, у).
Здесь p выражается через функции O(x) и f( 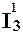 (x1, x2, x3),
(x1, x2, x3),  ( x1, x2, x3)), где f - это примитивно-рекурсивная функция из предыдущего примера.
( x1, x2, x3)), где f - это примитивно-рекурсивная функция из предыдущего примера.
3. Экспонента e(x) = 2x может быть задана соотношениями:
e(0) = S(0);
e(x+1) = 2×e(x).
Функции S(0(y)) и 2y - примитивно-рекурсивные. Поэтому функция e(x) также является примитивно-рекурсивной.
4. Функции sg(x) и 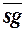 (x), определяемые как:
(x), определяемые как:
sg(x) = 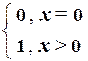 и
и 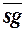 (x) =
(x) =  , задаются следующими схемами:
, задаются следующими схемами:
sg(0) = 0; 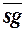 (x) = 1;
(x) = 1;
sg(x+1) = 1. 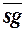 (x+1) = 0.
(x+1) = 0.
5. Функция уменьшения на единицу d(x) = x - 1 определяется как:
d(0) = 0;
d(x+1) = x.
6. Функция усеченного вычитания m(x, у) = x - у:
m (x, 0) = x;
m (x, у+1) = d(m(x, у)).
Функции из примеров 5 и 6 являются аналогами арифметического вычитания для множества целых неотрицательных чисел. Такие функции по определению равны нулю, если вычитаемое больше уменьшаемого.
Используя приведенные ранее функции, можно доказывать примитивную рекурсивность и других известных числовых функций.
Например, рассмотрим функцию mod(x,y), принимающую значение, равное остатку от деления числа x на число y.
Для определенности положим, что при делении на нуль остаток всегда равен 0.
Определим mod(x, y) схемой:
mod(0, y) = 0; (1)
mod(x+1, y) = (mod(x, y)+1)× sg(y - (mod (x, y)+1)). (2)
Здесь рекурсия ведется по первой переменной.
В соотношении (2) реализовано очевидное свойство остатка от деления значения x+1 на y, которое можно выразить следующим соотношением:
mod(x+1, y) либо равен mod(x, y)+1, если mod(x, y) < y, либо равен 0, в случае, когда mod(x, y) = y.
Аналогичными соотношениями можно выразить функцию для целочисленного деления div(x, y).
Для определенности будем считать, что div(x, 0) = x, поскольку функция целочисленного деления не является всюду определенной.
div(0, y) = 0;
div(x+1, y) = div(x, y)+ 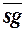 (y-(mod(x, y)+1)).
(y-(mod(x, y)+1)).
В приведенных определениях функций использовалась рекурсия по первой переменной. Это не соответствует схеме примитивной рекурсии, в которой переменная рекурсии - это последняя переменная определяемой функции. Тем не менее, рекурсия по первой переменной легко может быть сведена к рекурсии по последней переменной. Для этого достаточно выполнить перестановку переменных с помощью операции суперпозиции.
Например, для функцииmod(x, y) необходимо образовать вспомогательную функциюg(x, y)= mod( 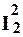 (x, y),
(x, y), 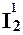 (x, y)). Такая функция может быть выражена с помощью схемы примитивной рекурсии.
(x, y)). Такая функция может быть выражена с помощью схемы примитивной рекурсии.
Поэтому mod также является примитивно-рекурсивной функцией, поскольку получается из примитивно-рекурсивной функции g обратной перестановкой переменных.
При обосновании примитивной рекурсивности некоторых функций могут оказаться полезными свойства, доказываемые в следующих теоремах.
Дата добавления: 2015-09-18; просмотров: 795;
