ЧАСТИЧНО РЕКУРСИВНЫЕ ФУНКЦИИ
Определим формальную систему, в которой определяются вычислимые числовые функции, отображающие числа из N или наборы чисел из N во множество N.
8.2.1. Простейшие функции
Следующие функции называются простейшими:
тождественный ноль О(x) = 0;
функция следования S(x) = x + 1;
функции проекции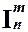 
(x1, ... , xn), где 1 
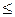m 
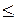n.
Все эти функции являются вычислимыми, поскольку могут вычисляться с помощью очевидных алгоритмов.
8.2.2. Элементарные функции
Пусть заданы функции:
f(x1, . . . , xk), gi(xi1, . . . , xim i), i = 1, . . . , k.
Функция h(xj1, . . . , xjr) получается из заданных функций с помощью операции суперпозиции, если её можно представить в виде выражения:
f(g1(x1,1, . . . , x1,m1), . . . , gk(xk,1, . . . , xk,mk)).
Здесь переменными функции h являются все различные переменные функций gi(xi,1, . . . , xi,mi), i = 1, . . . , k.
Если все функции f(x1, . . . , xn), gi(xi1, . . . , ximi), i = 1, . . . , k, являются вычислимыми, то вычислима и суперпозиция таких функций - функция h.
Дата добавления: 2015-09-18; просмотров: 516;