Построение минимального автомата
Пусть Â= (A, B, Q, j, y) - это произвольный автомат и Q = {q1, ... , qn}. Отношение неотличимости состояний автомата разбивает Q на классы неотличимых состояний: Q1, ..., Qd.
Определим множество состояний Q*={q1, . . . ,qd}. Содержательно всякое состояние qi соответствует классу неотличимых состояний Qi.
Определим две вспомогательные функции
h: Q ®{1, . . . , d} и x: {1, . . . , d}®{1, . . . , n}следующими соотношениями:
1) "qjÎ Q (h(qj) = i Û qjÎ Qi);
2) " j = 1, . . . ,d(x(j) = i Û i =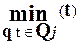 
).
Отображение h преобразует состояния автомата Â в номера классов неотличимых состояний, содержащих эти состояния.
Отображение h сопоставляет всякому классу неотличимых состояний состояние этого класса с наименьшим индексом.
Определим автомат Á= (A, B, Q*, F, Y). Функции F и Y этого автомата задаются соотношениями:
1) " a Î A, qiÎ Q*(F(a, qi) =qh(j(a,q x (i)));
2) " a Î A, qi ÎQ*(Y(a, qi) =y(a,qx(i))).
То есть всякий шаг работы автомата Á из состояния qi для произвольного входного символа аналогичен шагу работы автомата Âиз состояния qx(i) для такого же входного символа.
Указанное соответствие представлено на рис.7.8.
Qi
qx(i) qi
 Á
a(y(a,qx(i)))a(y(a,qx(i)))
Qr
j(a,qx(i))qr
Рис.7.8
При этом новое состояние qrавтомата Áопределяется классом Qj состояний автомата Â, который содержит состояние j(a,qx(i)).
2. Доказательство минимальности автомата Á
Докажем, что " 
Î A*(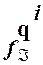 
( ) = 
( )).
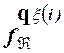Проведем доказательство этого свойства индукцией по длине слова . При этом дополнительно будет доказываться вспомогательное утверждение: если F*(a,qi)=qr, то j*(a,qx(i))ÎQr, а состояния j*(a,qx(i)) и qx(r) являются неотличимыми.
Дата добавления: 2015-09-18; просмотров: 753;