Индуктивный переход. Пусть = a - произвольное слово длины m = k+ 1
Пусть 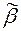 =
=  a - произвольное слово длины m = k+ 1. Тогда справедливы соотношения:
a - произвольное слово длины m = k+ 1. Тогда справедливы соотношения:
1) 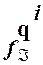 (
( 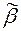 ) =
) = 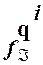 (
(  ) Y(a, F*(
) Y(a, F*(  , qi);
, qi);
2) 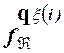 (
( 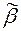 ) =
) = 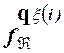 (
(  ) y(a, j*(
) y(a, j*(  ,qx(i))).
,qx(i))).
По индуктивному предположению 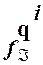 (
(  )=
)= 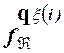 (
(  ).
).
Покажем, что y(a, F*(  , qi) = y(a, j*(
, qi) = y(a, j*(  ,qx(i))).
,qx(i))).
Пусть j*(  , qx(i)) = qj. Тогда из вспомогательного индуктивного предположения следует, что состояния qj и qx(r), где qr = F*(
, qx(i)) = qj. Тогда из вспомогательного индуктивного предположения следует, что состояния qj и qx(r), где qr = F*(  , qi) - неотличимые.
, qi) - неотличимые.
Поэтому справедливы равенства, доказывающие справедливость индуктивного перехода для основного свойства:
Y(a, F*(  , qi) = Y(a, qr) = y(a, qx(r)) = y(a, qj)= = y(a, j*(
, qi) = Y(a, qr) = y(a, qx(r)) = y(a, qj)= = y(a, j*(  ,qx(i))).
,qx(i))).
Покажем справедливость индуктивного перехода для вспомогательного утверждения.
Рассмотрим состояния j*(  a, qx(i)) и qx(h), где qh = F* (
a, qx(i)) и qx(h), где qh = F* (  a, qi). Покажем, что эти состояния неотличимые.
a, qi). Покажем, что эти состояния неотличимые.
Так как qj и qx(r) Î Qr, то состояния j*(  a, qx(i)) и j(a, qx(r)) являются неотличимыми.
a, qx(i)) и j(a, qx(r)) являются неотличимыми.
Так как qh = F*(  a, qi)= F(a, qr), то h = h(j(a, qx(r))).
a, qi)= F(a, qr), то h = h(j(a, qx(r))).
Следовательно, h = h(j(a,qj)).
Значит, j(a,qj), j(a, qx(j))Î Qh.
Поэтому состояния j*(  a, qx(i)) и qx(h), где qh =
a, qx(i)) и qx(h), где qh =
F*(  a, qi), являются неотличимыми.
a, qi), являются неотличимыми.
Дата добавления: 2015-09-18; просмотров: 1009;
