Свойство доказано. Покажем, что все состояния автомата Á являются отличимыми.
Покажем, что все состояния автомата Á являются отличимыми.
Пусть qi, qjÎ Q*. Тогда состояния qx(i) и qx(j) - отличимые. Поскольку 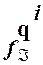 =
= 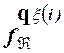 и
и 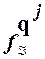 =
= 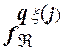 , то
, то 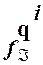 ¹
¹ 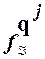 . Следовательно, состояния qi иqj также являются отличимыми.
. Следовательно, состояния qi иqj также являются отличимыми.
Поскольку "i( 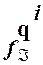 =
= 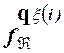 ) и "i(
) и "i( 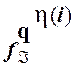 =
= 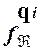 ), то множества функций, вычисляемых автоматами Áи Â, совпадают.
), то множества функций, вычисляемых автоматами Áи Â, совпадают.
Окончательно получаем, что автоматы Áи Â - эквивалентные, причем автомат Á - минимальный.
Дата добавления: 2015-09-18; просмотров: 627;
