Групова швидкість

Експериментально доведено, що будь-яка не синусоїдальна хвиля у лінійному середовищі може бути представлена сумою деяких синусоїдальних хвиль (принцип суперпозиції хвиль). Сукупність частот цих хвиль є лінійним спектром складного хвильового сигнала. Для графічного зображення спектра по осі ОХ відкладаються частоти спектра, а по осі OY їх амплітуди.

В нелінійному середовищі інформаційний сигнал завжди представляється у вигляді складної хвилі і може бути представлений як суперпозиція групи монохроматичних хвиль, що поширюються у середовищі з різними швидкостями. При цьому пакет "розпливається" - форма сигналу змінюється з часом. Для розуміння сутності процесу передачі інформації у часі, покладемо, що такий сигнал, як деяке значення величини амплітуди, передається за допомогою суперпозиції лише двох хвиль з близькими частотами 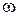та w+dw (dw<<w) і хвильовими числами k та k+dk (dk<<k) у вигляді

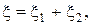(1)

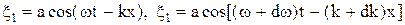. (2)

Результат додавання таких хвиль дає

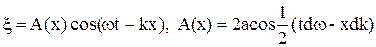. (3)

Швидкість передачі сигналу у вигляді деякої сталої амплітуди, називається груповою швидкістюі вона визначається рівнянням

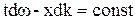. (4)

Варіація 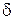по змінним t та x від (4) дає таке рівняння

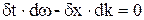. (5)

З (5) знайдемо групову швидкість u - швидкість поширення сталої амплітуди

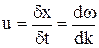. (6)

Групова швидкість u реальному середовищі може бути визначена через фазову швидкість V та довжину хвилі l так

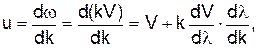
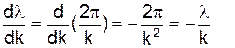
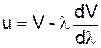. (7)

Коли фазова швидкість є зростаючою функцією l, то 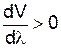(нормальна дисперсія) і групова шкидкість менше фазової u<V, а для спадної функції ¾ u>V. У разі відсутності дисперсії 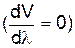групова та фазова швидкості будуть однаковими u=V.