Перетворення Лоренця для координат
Розглянемо дві інерційні системи відліку, одна з яких K' рухається відносно іншої K із швидкістю 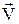 (V=const і V £ c) паралельно осі ОХ. Якщо покласти, що перетворення координат, подібно до перетворень Галілея, лінійне, то потрібно, щоб при прямому перетворенні було:
(V=const і V £ c) паралельно осі ОХ. Якщо покласти, що перетворення координат, подібно до перетворень Галілея, лінійне, то потрібно, щоб при прямому перетворенні було:
x = g(x' + Vt'), (1)
а зворотному:
x' = g(x - Vt). (2)
Інші координати повинні співпадати:
y = y', z = z'.
Використовуючи постійність швидкості світла та рівняння (1) і (2), знайдемо величину 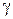 та рівняння перетворення часу.
та рівняння перетворення часу.
Нехай початки відліку систем K та K' у момент часу посилання світлового сигналу співпадають. Згідно другого постулату, шлях, що пройде сигнал у системі К буде x=ct, а в системі K' ¾ x'=ct'. Підставимо ці значення в рівняння перетворення координат:
сt=g(ct' + Vt'), (3)
сt'=g(ct - Vt). (4)
Перемноживши ліві та праві частини (3) та (4), після скорочення, одержимо:
g2 = 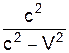 =
= 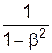 , де b =
, де b = 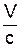 , g =
, g = 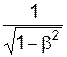 > 1. (5)
> 1. (5)
Для встановлення зв'язку між t та t' підставимо в x'= g(x - Vt) значення для x: x' = g [g(x' + Vt') - Vt]. Проведемо послідовні розрахунки
x' = g [g(x' + Vt') - Vt] = g2x' + g2Vt' - gVt,
gVt=(g2 - 1)x' + g2Vt' = g2(V2/c2)x' + g2Vt',
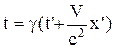 . (6)
. (6)
В (6) ми врахували, що
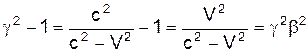 .
.
Подібно можна одержати зворотне перетворення
t' = g(t - Vx/c2). (7)
Як видно з одержаних виразів, час у різних інерційних системах протікає по різному, тому твердження про проміжок часу між двома подіями має сенс тільки при посиланні на певну інерційну систему відліку.
Запишемо одержані вирази для прямих та зворотних перетворень у вигляді таблиці:
| Прямі перетворення | Зворотні перетворення |
| x = g(x' + Vt') | x' = g(x - Vt) |
| y = y', | y' = y |
| z = z' | z' = z |
t = g(t' + 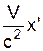 ) )
| t' = g(t - 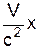 ) )
|
Якщо V << c, то g=1 і t=t' і перетворення Лоренця перейдуть у перетворення Галілея і ми перейдимо до класичної механіки.
3.3. Перетворення швидкостейу релятивістській механіці
Якщо зважити на те, що компоненти швидкостей тіла в системі K визначаються як Ux = 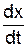 , Uy =
, Uy = 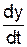 , Uz =
, Uz = 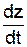 , а в системі K' ¾
, а в системі K' ¾ 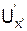 =
= 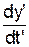 , U'y' =
, U'y' = 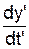 , Uz' =
, Uz' = 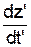 , а диференціали dx = g(dx' + Vdt'), dt = g(dt' + Vdx/c2), dy =dy', dz = dz' та dx' = g(dx - Vdt), dt' = g(dt - Vdx'/c2), то пряма підстановка дає перетворення швидкостей у вигляді:
, а диференціали dx = g(dx' + Vdt'), dt = g(dt' + Vdx/c2), dy =dy', dz = dz' та dx' = g(dx - Vdt), dt' = g(dt - Vdx'/c2), то пряма підстановка дає перетворення швидкостей у вигляді:
Uх= 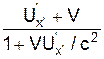
| 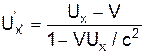
|
Uy = Uy'· 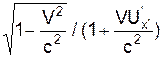
| U'y' = Uy· 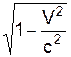 /(1 - VUx/c2) /(1 - VUx/c2)
|
Uz = Uz'· 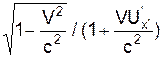
| U'z' = Uz· 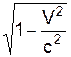 /(1 - VUxc2) /(1 - VUxc2)
|
Наприклад, якщо тіло рухається із швидкістю U вздовж осі ОХ, то її перетворення через швидкість U'
у класичній механіці:
U = U' + V,
в релятивістській механіці:
U = (U+V)/(1+VU/c2).
Якщо U' = c, то U = (c+V)/(1+Vc/c2) = c, як того і вимагає постулат Ейнштейна.
3.4. Інтервалміж подіями та його інваріантність
Якщо відомі координати двох подій x1, y1, z1, t1 i x2, y2, z2, t1, то величина
s12= 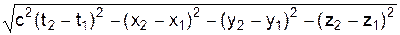
називається інтервалом між цими подіями. Інтервал між двома близькими подіями
ds= 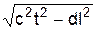 , де dl2=dx2+dy2+dz2.
, де dl2=dx2+dy2+dz2.
Інтервал s12 між двома подіями однаковий за величиною в усіх інерційних системах відліку (інваріантність s12). Розглянемо це питання докладніше.
Інтервал у рухомій системі відліку К' буде s'2=c2t'122 -l'2, l2=x122+ y122+z122. Проведемо очевидні послідовні перетворення співвідношення c2t12'-x12'2 із врахуванням перетворень Лоренця:
c2t12'-x12'2 = c2g2(t12 - V x12/c2)2 - g2(x12 - Vt12)2 =
c2g2(t122 + V2 x122 /c4 - 2 t12 x12V/c2) - g2(x122 + V2t122 - 2 x12Vt12) =
c2g2(t122+ x122V2 /c4 ) - g2(x122+V2t122 ) = g2[c2t122+ x122V2 /c2- x122 -V2t122]=
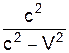 [ t122(c2-V2)- x122(1- V2 /c2)]= c2 t122 - x122.
[ t122(c2-V2)- x122(1- V2 /c2)]= c2 t122 - x122.
Остаточно маємо:
s'2=c2t'122 -l'2 = s2 = c2t122 -l2 = inv.
Часоподібнийінтервал. Якщо s122 ³0, то інтервал s12 називається часоподібним, і для нього існує така система відліку K', в якій дві події відбуваються в одній точці простору x1' = x2', y1' = y2', z1' = z2', а час, що пройшов між ними t12' = s12/c.
Простороподібнийінтервал. Якщо s122 <0, то інтервал s12 називається простороподібним, і для нього не існує система відліку K', в якій дві події відбуваються в одній точці простору, але існують системи відліку, в яких вони відбуваються одночасно.
Дата добавления: 2015-09-18; просмотров: 671;
