Власна довжина

Власна довжина¾ це лінійний розмір L₀ тіла в тій системі відліку, де воно знаходиться в стані спокою. Довжина L₀ нерухомого тіла, виміряна в системі K' у напрямку її руху відносно системи K із швидкістю V у момент часу t₁=t₂=t, більша довжини тіла L, що виміряна в системі K.

Дійсно,

L₀ = x₂' - x₁' = g(x₂ - Vt) - g(x₁ - Vt) = g(x₂ - x₁) = gL, g = ,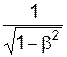

L = L₀ .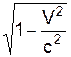

Звідси видно, що L < L₀.

3.7. Основне рівняння релятивістської динаміки

3.7.1. Релятивістська маса

Наведемо без доведення вираз для маси тіла, що залежить від швидкості тіла, так називаної релятивістської маси

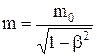. (1)

У цьому виразі m₀ - маса спокою, тобто маса нерухомого тіла, b - відношення швидкості тіла V до швидкості світла у вакуумі с.

3.7.2. Релятивістський імпульс

Імпульс визначається як добуток релятивістської маси на швидкість тіла

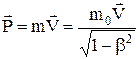. (2)

3.7.3. Основне рівняння динаміки

Основне рівняння динаміки має вигляд такий як і в класичній динаміці, коли воно записується через імпульс

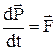, (3)

де 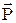- релятивістський імпульс(2).

Підставимо в (3) вираз (2) і проведемо диференціювання

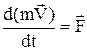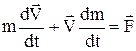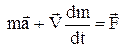, , . (4)

У (4) поряд з доданком 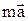стоїть доданок, залежний у неявному вигляді від часу. Цей доданок становиться рівним 0 тоді коли вектор сили перпендикулярний швидкості. У цьому випадку сила є поперечною і під її дією змінюється лише напрямок швидкості і 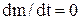. При цьому вектор прискорення співпадає за напрямком з вектором сили. Таке співпадання буде і при паралельності векторів сили та швидкості.

3.8. Енергія тіла

В релятивістській механіці крім постулатів Ейнштейна виконуються закони збереження імпульсу, моменту імпульсу, закон збереження енергії але не виконується закон збереження маси тіла. Наприклад, при розпадах ядра на складові частинки їх сумарна маса може бути меншою або більшою маси тіла. Це пов'язано з тим, що такі розпади можуть відбуватися з виділенням або поглинанням ядром енергії.

Робота сили 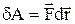по переміщенню вільної частинки, як і в класичній механіці йде на приріст її кінетичної енергії T, тобто dА=dT. Для знаходження Т, зробимо ряд послідовних очевидних перетворень:

,

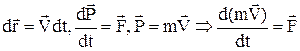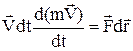
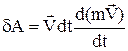, dT=dA,

,

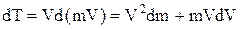В той же час

, , ,

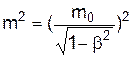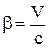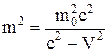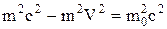. (1)

Знайдемо диференціал від (1), вважаючи, що m та V змінюються з часом та виконаємо елементарні перетворення

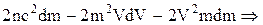
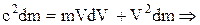
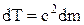. (2)

Маса тіла зростає від маси спокою 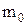до релятивістської маси m, тому у (2) можна виконати інтегрування у межах цих мас

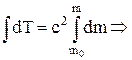
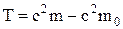. (3)

Покладемо в (3) 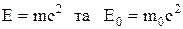. У класичній механіці кінетична енергія та потенціальна енергіяскладають повну механічну енергію тіла. В релятивістській механіці також визначають повну механічну енергію тіла, яка є сумою енергії 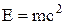та потенціальної енергії тіла у силовому полі.

3.8. Зв'язок енергії та імпульсу

Знайдемо значення та доведемо незмінність у різних системах відліку, тобто інваріантність, виразу E²-p²c². Для цього проведемо ряд послідовних очевидних перетворень:

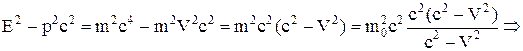
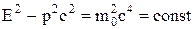, (1)

що й треба було довести.

Звідси установимо зв'язок енергії та імпульсутіла

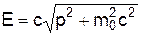. (2)

Знайдемо зв'язок імпульсу та кінетичної енергії Т тіла:

,

,

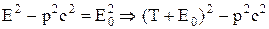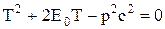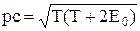. (3)

3.9. Зв'язок маси та енергії спокою

Зв'язок маси та енергії спокою, що задається виразом Е₀ = m₀c² указує, що сумарна маса взаємодіючих частинок, на противагу класичній механіці, не зберігається. Наприклад, при абсолютно не пружному ударі двох однакових частинок із масами m₀, що рухаються одна назустріч іншій, утвориться нова нерухома частинка з масою М. Енергії частинок до співударяння 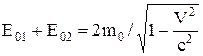, а після співударяння Е₀ = Мс². Згідно

закону збереження енергії Мс² = 2m₀с²/ 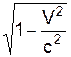і тоді М = 2m₀/ 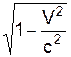> 2m, тобто маса утвореної частинки більше сумарної маси двох однакових, з яких вона утворилася. Це сталося тому, що кінетична енергія частинок перетворилася в еквівалентну кількість енергії спокою, що й призвело до зростання маси на Dm = DE₀/c².

Іншим прикладом є взаємозв'язок між енергією зв'язку Е_зв нуклонів (протонів та нейтронів) у ядрі та різницею (дефектом) мас Dm між масою ядра і сумарною масою нуклонів ядра E_зв = Dmc².