Постановка задачи для уравнения эллиптического типа

Классическим примером уравнения эллиптического типа является уравнение Пуассона

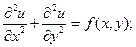
или уравнение Лапласа, 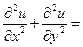0,

которое получается из уравнения Пуассона при f(x, t) º 0.

Здесь функция u(x, t) может иметь различный физический смысл, например, описывать стационарное, независящее от времени распределение температуры, скорость потенциального (безвихревого) течения идеальной (без трения и теплопроводности) жидкости, распределение напряжённостей электрического и магнитного полей, распределение потенциала поля тяготения и т.п.

Первая краевая задача. Если на границе Г расчётной области = + Г (в данном случае расчётная область 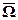– это сама область 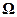, включая её границу Г) задана искомая функция, то соответствующая первая краевая задача для уравнения Лапласа или Пуассона называется задачей Дирихле:

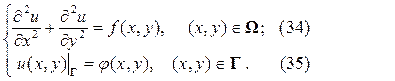
Вторая краевая задача. Если на границе Г расчётной области задаётся нормальная производная искомой функции, то соответствующая вторая краевая задача называется задачей Неймана для уравнения Лапласа или Пуассона:

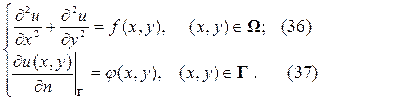
здесь n - направление внешней к границе Г нормали.

Иногда краевое условие (37) записывают в более удобном виде:

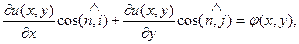
где 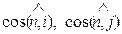- направляющие косинусы внешнего вектора единичной нормали к границе Г, i и j орты базисных векторов.

Третья краевая задача для уравнения Пуассона (Лапласа) имеет вид:

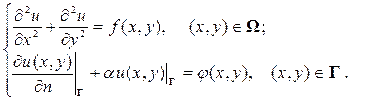
Замечание. Следует отметить, что в вышеперечисленных постановках задач математической физики число начальных условий равно порядку дифференциального уравнения по времени, а старший порядок производной по времени в начальных условиях на единицу меньше порядка дифференциального уравнения по времени.

Старший порядок производной по пространственной переменной в краевых условиях равен порядку дифференциального уравнения по пространственной переменной минус единица.

В одномерных задачах с одной пространственной переменной количество граничных условий точно равно порядку дифференциального уравнения по пространственной переменной.

Количество краевых условий для многомерных задач не ограничено, поскольку на разных участках границы могут быть заданы граничные условия различного рода.

Заключение (план - аннотация лекции №27).

Лекция 27 посвящена введению в приближённые методы решения дифференциальных уравнений с частными производными.

Отмечено, что при математическом анализе физических процессов, когда исследуемые свойства объекта описываются функциями не одной, а несколькими переменными, то при составлении математических моделей изучаемых явлений вместо обыкновенных дифференциальных уравнений возникают уравнения с частными производными.

В качестве примеров уравнений математической физики, наиболее востребованных на практике, рассмотрены уравнение Лапласа, уравнение Пуассона, уравнение теплопроводности (Фурье), волновое уравнение, уравнение Гельмгольца, телеграфное уравнение, уравнение переноса, уравнение акустики.

Приведена классификация уравнений с частными производными второго порядка, в основу которой положен анализ знака дискриминанта обобщённого уравнения второго порядка с частными производными.

Дана классификация методов решения уравнений с частными производными.

Обсуждаются подходы к постановке задач для уравнений математической физики. При этом корректность постановки задач связываемая с требованиями разрешимости; однозначности; непрерывной зависимости от исходных данных (иначе, устойчивости).

Рассмотрены примеры постановки задач для уравнений математической физики гиперболического, параболического и эллиптического типов.

Литература:

1. И.С. Березин, Н.П. Жидков. Методы вычислений. Т. 2. – М.: Физматгиз, 1962. – 620 с.

2. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.

3. В.Ф. Формалёв, Д.Л. Ревизников. Численные методы. – М.: Физматлит, 2004. 400 с.

4. Б.П. Демидович, И.А. Марон, Э.З. Шувалова. Численные методы анализа.
– М.: Наука, 1967. – 368 с.

5. Н.В. Копчёнова, И.А. Марон. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 368 с.