Постановка задачи для уравнения параболического типа

Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). Как отмечалось выше, в одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид:

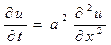, 0 < x < l, t >0 (15)

Уравнение (15), например, может описывать распространение тепла в тонком стержне длиной l, теплоизолированном по боковой поверхности. При этом функция u(x, t) задаёт значение температуры в любой точке стержня в произвольный момент времени t, при условии, что известно распределение температуры в стержне в начальный момент времени t = 0 и известна температура на концах стержня x = 0 и x = l в любой момент времени t. Таким образом, постановка задач для уравнения теплопроводности имеет следующий вид.

Первая начально-краевая задача. Если на границах стержня x = 0 и x = l заданы краевые условия первого рода, т.е. для любых моментов времени на концах стержня x = 0 и x = l заданы значения искомой функции u(x,t) (т.е. температуры):

u(0, t) = j ₁(t), x = 0, t >0, (16)

u(l, t) = j ₂(t), x = l, t >0, (17)

и, кроме того, для функции u(x, t) заданы начальные условия, т.е. задано распределение температуры в любой точке стержня в момент времени t = 0:

u(x, 0) = y (x), 0 £ x £ l (18)

то задачу (15) – (17) называют первой начально-краевой задачей для уравнения теплопроводности.

В терминах теории теплообмена функция u(x,t) описывает распределение температуры в пространственно-временной области W´T = {0 £ x £ l, 0 £ t £ T}, параметр а² – является коэффициентом температуропроводности, а краевые условия (16), (17) с помощью функций j ₁(t) и j ₂(t) задают температуру на границах
x = 0, x = l для различных моментов времени.

Вторая начально-краевая задача. Если на границах x = 0 и x = l заданы краевые условия второго рода, т.е. для x = 0 и x = l заданы значения производных искомой функции по пространственной переменной:

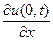= j ₁(t), x = 0, t >0, (19)

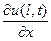= j ₂(t), x = l, t >0, (20)

u(x, 0) = y (x), 0 £ x £ l (21)

и, кроме того, для функции u(x, t) заданы начальные условия (21), то задачу (15), (19) – (21) называют второй начально-краевой задачей для уравнения теплопроводности. В терминах теории теплообмена граничные условия (19), (20) задают тепловые потоки на концах стрежня для различных моментов времени.

Третья начально-краевая задача. Если на границах x = 0 и x = l заданы краевые условия третьего рода, т.е. для x = 0 и x = l заданы линейные комбинации искомой функции и её частной производной по пространственной переменной:

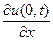+ a u(0, t) = j ₁(t), x = 0, t >0, (22)

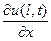+ b u(l, t) = j ₂(t), x = l, t >0, (23)

и, для функции u(x, t) заданы начальные условия (21), то задачу (15), (22), (23) называют третьей начально-краевой задачей для уравнения теплопроводности.

В терминах теории теплообмена граничные условия (22), (23) задают теплообмен между газообразной и жидкой средой (которые располагаются с разных «торцов» стержня) и границами расчётной области (т.е. внутренней частью стержня). Из-за теплообмена, температуры u(0, t) и u(l, t) на торцах стержня не известны, а известно, что температуры газообразной и жидкой среды соответственно равны
j ₁(t)/a и j ₂(t)/b. Параметры a и b являются коэффициентами теплообмена между газообразной или жидкой средой и соответствующей границей стержня.