Постановка задачи для уравнения гиперболического типа

Классическим примером уравнения гиперболического типа является волновое уравнение, которое имеет вид:

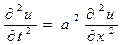, 0 < x < l, t >0 (24)

В данном случае искомая функция u(x, t) описывает малые продольные или поперечные колебания стержня или туго натянутой струны, точкам которых в начальный момент времени t =0 сообщили начальное смещение y₁(t)и скорость y₂(t). В случае продольных колебаний параметр a характеризует скорость звука в материале, из которого изготовлен стержень, а для поперечных колебаний параметр a связан с массой единицы длины струны и силой её натяжения.

Первая начально-краевая задача. Если концы стержня движутся по заданным законам, то есть на концах заданы перемещения (значения искомой функции), то первая начально-краевая задача для волнового уравнения имеет вид:

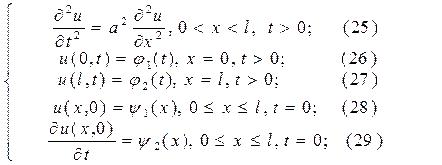
Если концы стержня жестко закреплены, то j ₁(t) = j ₂(t) = 0.

При постановке первой начально-краевой задачи для волнового уравнения условием (28) задаётся начальное распределения значений искомой функции u(x, t) (характеризующей смещение точек стрежня или струны), а условием (29) задаётся ещё и начальная скорость такого смещения.

Вторая начально-краевая задача. Если на концах стержня заданы значения силы, которая по закону Гука пропорциональна производной перемещения по пространственной переменной (т.е. на концах заданы значения первых производных по пространственной переменной x), то ставится вторая начально-краевая задача для волнового уравнения:

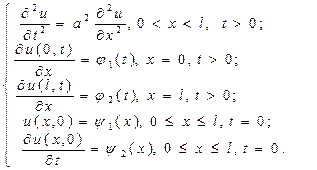
В условиях, когда концы стержня свободны, то функции j ₁(t) = j ₂(t) = 0.

Третья начально-краевая задача. Если концы стержня или струны закреплены упруго, т.е. на концевые заделки действуют силы, пропорциональные перемещениям, то ставится третья начально-краевая задача для волнового уравнения

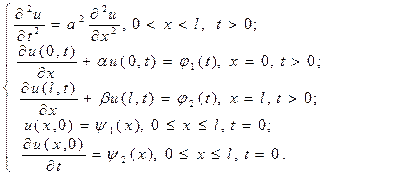
Аналогично ставятся двумерные трехмерные начально-краевые задачи для двумерного и трёхмерного волнового уравнения.

Замечание. Необходимо отметить, что волновое уравнение (24) легко трансформируется в систему уравнений акустики (13), являющихся простейшей линейной моделью газодинамических течений. Действительно, введём следующие обозначения:

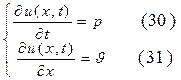
Продифференцируем уравнение (30) по переменной t, а уравнение (31) по переменной x и подставим результат в волновое уравнение 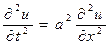, при этом получим:

(32)

Далее продифференцируем уравнение (30) по переменной x, а уравнение (31) по переменной t ,в результате будем иметь:

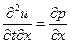и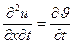

Полагая далее, что смешанные производные от u(x, t) по переменным x и t не зависят от порядка дифференцирования, получим:

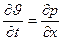(33)

Полученную систему уравнений (32), (33):

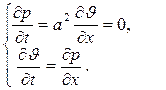
называют уравнениями акустики, как уже отмечалось выше, функции p и J характеризуют возмущения (т.е. слабые колебания) давления и скорости в акустической волне.