Конечноразностные формулы численного дифференцирования на основе интерполяционных полиномов
2.1 Построение формул численного дифференцирования на основе первой интерполяционной формулы Ньютона.
Пусть дифференцируемая функция y = f(x) задана своими значениями
y0, y1, y2, …, yn, на сетке равноотстоящих узлов 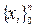 : x0, x1, x2, …, xn отрезка [a, b], т.е. в данном случае:
: x0, x1, x2, …, xn отрезка [a, b], т.е. в данном случае:
xi = x0 + ih, где i = 1, 2, …, n,
где h > 0 - шаг сетки (или таблицы).
Для нахождения на отрезке [a, b] значений производных y¢ = f¢ (x), y¢¢ = f¢¢ (x) и т.д., функцию y = f(x) в узлах отрезка [a, b] (приближённо) заменяют первым интерполяционным полиномом Ньютона, построенным для данной системы равноотстоящих узлов 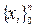 .
.
y(x) » Pn(x0 +qh) = y(x0) + qDy0 + 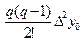 + + 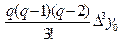 + + 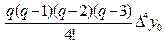 + …+ + …+ 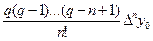
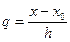 , h = x i+1 - x i; i = 1, 2, …, n. , h = x i+1 - x i; i = 1, 2, …, n.
| (4) |
Производя перемножение биномов в формуле (4) получим:
y(x) » y(x0)+ qDy0 + 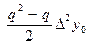 +
+ 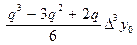 +
+ 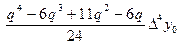 + … (5)
+ … (5)
Поскольку 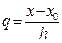 , то в соответствии с выражениями (4) и (5) функцию Pn(x0 + qh) можно рассматривать как сложную функцию переменной x. Поэтому в соответствии с правилом дифференцирования сложной функции имеем:
, то в соответствии с выражениями (4) и (5) функцию Pn(x0 + qh) можно рассматривать как сложную функцию переменной x. Поэтому в соответствии с правилом дифференцирования сложной функции имеем:
f¢x(q(x)) @ [Pn(x0 +q(x)h)]¢x = [Pn(x0 +q(x)h)]¢q ×q¢x, где q¢x 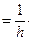
и, выполняя дифференцирование формулы (5), получаем:
yx¢(x) = y¢q(x0 + q(x)h)×q¢x @ 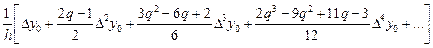
| (6) |
Далее по аналогии с выражением (6) для y¢(x) можно написать выражение для y²(x) и y¢¢¢(x):
y¢¢(x) @ 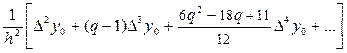 (7)
(7)
y¢¢¢(x) @ 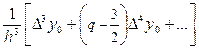 (8)
(8)
Таким же образом в случае необходимости можно вычислить и производные функции y(x) любого порядка.
Наиболее важной в приложенияхявляется простейшая формула для аппроксимация второй производной с помощью разностного отношения:
y¢¢(x) » 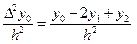 . (9)
. (9)
Формула (9) получается из выражения (5) при n = 2, на промежутке x Î(x0, x2).
Аппроксимация второй производной в виде разностного отношения (9) часто востребована при построении конечноразностных методов решения краевых задач для обыкновенных дифференциальных уравнений второго порядка и при разработке численных методов решения уравнений в частных производных.
Замечание. Приводимые здесь рассуждения и выкладки имеют смысл только в том случае, когда заранее известно, что для функции y = f(x) в принципе существуют производные рассматриваемых порядков, т.е. мы заранее из каких-либо соображений знаем степень гладкости функции y = f(x).
2.2 Численное дифференцирование в узловых точках таблицы.
Иногда требуется находить производные функции y(x) в самих табличных точках x i (т.е. узлах сетки). В этом случае формулы численного дифференцирования упрощаются.
При построении интерполяционного полинома Ньютона каждое табличное значение xi, в котором нужно вычислить значение производной f¢ (xi), может быть принято за базовый узел x0. Поэтому в случае, когда базовым узлом x0 является узел xi, переменная 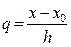 в формулах (6) – (8) будет равна
в формулах (6) – (8) будет равна 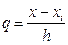 и формулы (6) – (8) перепишутся в виде:
и формулы (6) – (8) перепишутся в виде:
y¢(x) @ 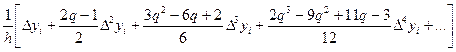 ;
y¢¢(x) @ ;
y¢¢(x) @ 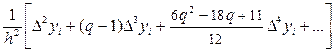 ;
y¢¢¢(x) @ ;
y¢¢¢(x) @ 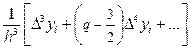 ;
где ;
где 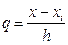 . .
| (10) |
Формулами (10) задаются выражения для аппроксимации производных y¢(x), y¢¢(x), y¢¢¢(x) функции y = f(x) вблизи табличной точки x i, y(xi).
При подстановке в формулы (10) вместо x значения базового узла xi
(x = xi) переменная 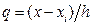 обращается в нуль и для значений производных в узлах таблицы, т.е. в точках x = x i получим следующие выражения:
обращается в нуль и для значений производных в узлах таблицы, т.е. в точках x = x i получим следующие выражения:
y¢(xi) @ 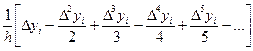 (11)
(11)
y¢¢(xi) @ 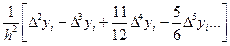 (12)
(12)
y¢¢¢(xi) @ 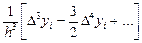 (13)
(13)
Чтобы построить аппроксимации (11) - (13) для y¢(xi) и y¢¢(xi), включающие, например, конечные разности пятого порядка, нужно по формулам (4) или (5) построить первый интерполяционный полином Ньютона пятого порядка (n = 5), выбрав в качестве базового узла точку xi. Отметим, что в этом случае для вычисления значений конечных разностей Dyi, D2yi, D3yi, D4yi, D5yi необходимо использовать шесть строк из таблицы значений функции y = f(x):
y(xi), ® y(xi+1), ® y(xi+2), ® y(xi+3), ® y(xi+4), ® y(xi+5).
Формулы численного дифференцирования (10) - (13), построенные на основе первой интерполяционной формулы Ньютона, более эффективны для использования в начальной части таблицы значений функции, т.е. когда в таблице значений функции «ниже» базового узла xi имеется достаточное количество строк, необходимых для вычисления соответствующих значений конечных разностей.
Аналогичные формулы численного дифференцирования могут быть получены и на основе второй интерполяционной формулы Ньютона. Они более эффективны при выборе базовых узлов в конечной части таблицы значений функции. Также можно вывести и ряд «центральных» формул численного дифференцирования на основе рассмотренных ранее интерполяционных формул Гаусса, Бесселя, Стирлинга, такие формулы более эффективно «работают» в близи центральных узловых точек таблицы значений функции [1, стр. 567 - 570].
Практические рекомендации по использованию конечноразностных формул численного дифференцирования.
1. Для нахождения значений производных y¢(x), y¢¢(x), y¢¢¢(x) … функции y(x) в некоторой фиксированной (межузловой) точке x* таблицы значений функции
y = f(x) в качестве базового узла xi в формулах (10) необходимо выбрать ближайшее к x* табличное значение аргумента xi (лежащее левее точки x*).
2. При желании получить аппроксимации производных y¢(x), y¢¢(x), y¢¢¢(x) … с наибольшей точностью максимальный порядок конечных разностей в формулах (10) - (13) определяется при построении таблицы конечных разностей функции y = f(x). При этом, исходя из анализа таблицы конечных разностей, необходимо оценить оптимальную степень n интерполирующего полинома Pn(x) и сохранить в формулах (10) - (13) конечные разности до Dnyi включительно.
3. Отметим, что занижение степени интерполирующего полинома Pn(x) (4) - (5) отрицательно сказывается на точности полученных формул численного дифференцирования так же, как и необоснованное завышение его степени. Завышение степени полинома выше оптимальной приводит к учёту в формулах численного дифференцирования ошибок округления. Это происходит потому, что из-за ограниченной точности задания значений сеточной функции y(x) конечные разности высоких порядков начинают возрастать с увеличением их порядка вследствие «расползания» исходных ошибок округления и, следовательно, конечны разности высоких порядков могут содержать большие ошибки.
2.3 Связь приближённых значений производной функции с узловыми значениями самой функции.
Адаптируем полученную выше формулу численного дифференцирования:
y¢(x) @ 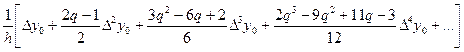 (6)
(6)
для наиболее часто используемых практических ситуаций.
Если показатель - n степени интерполяционного полинома Ньютона (5), лежащего в основе формулы (6), зафиксировать соответственно равным: n = 1, n = 2, n = 3, то это будет соответствовать ситуации, когда дифференцируемая функция y = f (x) на отрезке интерполирования заменяется соответственно:
a. прямой (n = 1) - случай линейной интерполяции по двум точкам x0; x1;
b. параболой (n = 2) - случай квадратичной интерполяции по трём точкам x0; x1; x2;
c. кубической параболой (n = 3) - случай кубической интерполяции по четырём точкам x0; x1; x2; x3.
Для рассматриваемых случаев из формулы (6) получаются следующие выражения для приближённых значений производной y¢(x) функции y = f (x):
 для x Î[x0; x1] (14)
для x Î[x0; x1] (14)
– оценка (аппроксимация) производной на основе линейной интерполяции.
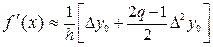 для x Î[x0; x2] (15)
для x Î[x0; x2] (15)
– оценка (аппроксимация) производной на основе квадратичной интерполяции.
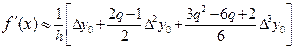 для x Î[x0; x3] (16)
для x Î[x0; x3] (16)
– оценка (аппроксимация) производной на основе кубической интерполяции.
Получим на основе формул (14) – (16) аппроксимации для y¢(x) = f¢ (x) в узлах интерполяции, выраженные через значения функции y = f (x) в узлах сетки. Для этого учтём, что при подстановке в формулы (14) - (16) вместо переменной x узловых значений x0, x1, x2; x3 переменная 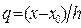 будет соответственно равна: 0, 1, 2, 3.
будет соответственно равна: 0, 1, 2, 3.
a) Случай линейной интерполяции: n = 1, x Î[x0; x1].
В этом случае на отрезке [x0; x1] функция y = f (x) заменяется прямой линией P1(x0 + qh) = y(x0)+ qDy0, проходящей через точки x0 и x1, а её производная (6) приближённо заменяется выражением: 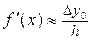 , где Dy0 = y(x1) – y(x0)
, где Dy0 = y(x1) – y(x0)
Поэтому из (6) в данном случае имеем:
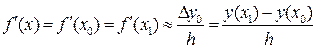 (17)
(17)
б) Случай квадратичной интерполяции: n = 2, x Î[x0; x2].
В этом случае на отрезке [x0; x2] функция y = f (x) заменяется параболой:
P2(x0 +qh) = y(x0)+ qDy0 + 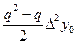 ,
,
проходящей через точки x0, x1, x2, а её производная f¢ (x) (6) заменяется выражением:
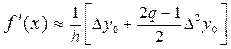 , где Dy0 = y(x1) – y(x0); D2y0 = y(x2) – 2y(x1) + y(x0);
, где Dy0 = y(x1) – y(x0); D2y0 = y(x2) – 2y(x1) + y(x0);
Откуда, учитывая, что при x = x0 q = 0, а при x = x1 q = 1, при x = x2 q = 2, получаем:
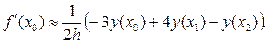 (18)
(18)
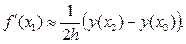 (19)
(19)
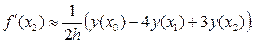 (20)
(20)
в) Случай кубической интерполяции: n = 3, x Î[x0; x3].
В этом случае на отрезке [x0; x3] функция y = f (x) заменяется кубической параболой, проходящей через точки x0, x1, x2, x3:
P3(x0 + qh) = y(x0) + qDy0 + 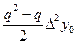 +
+ 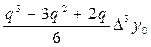 ,
,
а её f¢ (x) (6) заменяется выражением:
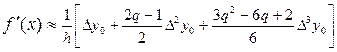 ,
,
где Dy0 = y(x1) – y(x0); D2y0 = y(x2) – 2y(x1) + y(x0); D3y0 = y(x3) – 3y(x2) +3y(x1) – y(x0);
Так как при x = x0 q = 0, при x = x1 q = 1, при x = x2 q = 2, при x = x3 q = 3, получаем:
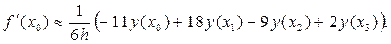 (21)
(21)
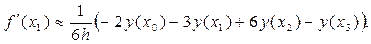 (22)
(22)
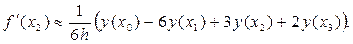 (23)
(23)
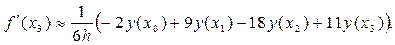 (24)
(24)
Дата добавления: 2015-09-14; просмотров: 1673;
