Оптимизация шага численного дифференцирования при ограниченной точности задания значений функции
При рассмотрении данного вопроса будем считать что yi – это приближённое значение функции f(xi), т.е. yi – это значение функции f(xi), полученное путём вычисления и представленное в таблице с конечной заданной точностью. Предположим, что уровень абсолютных погрешностей значений yi в разных узлах сетки (таблицы) примерно одинаков и ограничен числом d > 0, поэтому, в данном случае имеем:
f(xi) » yi ± d, т.е. f(xi) Î(yi - d, yi + d).
Будем изучать влияние неточностей задания (вычисления) значений функции на результаты аппроксимации производных (по этим значениям) для различных простейших формул численного дифференцирования [2, стр. 524].
Рассмотрим простейшую формулу (28) аппроксимации первой производной в узле xi правым разностным отношением:
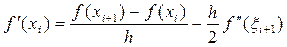 , x i+1 Î(xi; xi+1)
, x i+1 Î(xi; xi+1)
При вычитании приближённых чисел их абсолютные погрешности складываются, поэтому замена неизвестного точного разностного отношения 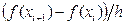 реально вычисляемым отношением
реально вычисляемым отношением 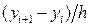 порождает (вычислительную) ошибку, аппроксимации производной, оцениваемую по модулю величиной
порождает (вычислительную) ошибку, аппроксимации производной, оцениваемую по модулю величиной 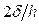 .
.
В соответствии с формулой (28) погрешность метода аппроксимации f¢(x) точным разностным отношением 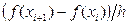 можно оценить величиной
можно оценить величиной 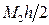 , где
, где 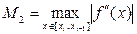 . Поэтому при оценке полной погрешности аппроксимации производной f¢ (x) приходим к неравенству:
. Поэтому при оценке полной погрешности аппроксимации производной f¢ (x) приходим к неравенству:
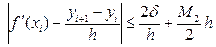 . (53)
. (53)
Итак, полная абсолютная погрешность приближённого равенства:
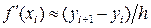 (54)
(54)
оценивается величиной: 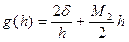 , (55)
, (55)
которая образована двумя слагаемыми:
- вычислительной погрешностью, порождаемой неточными значениями функции;
- погрешностью аппроксимации, связанной с выбором формулы численного дифференцирования.
Схематично, поведение графика функции g = g(h) отображено на рис. 3.
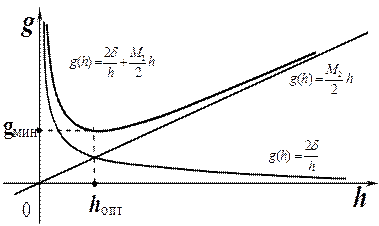
Рисунок - 3 зависимость границы полной погрешности g(h)
приближённого равенства (54) от шага h.
Из (55) следует, что при h ® 0 за счёт первого слагаемого g(h) бесконечно растёт (поскольку 2d - постоянная величина не зависящая от шага сетки). Поэтому при сравнительно больших h с ростом h также будет наблюдаться и рост g(h) (асимптотически линейный), благодаря второму слагаемому.
Понятно, что функция g = g(h) имеет минимум, т.е. существует такое значение h = hопт, при котором верхняя граница g(h) полной погрешности приближённого равенства (54) минимальна. Это значение легко найти, приравнивая нулю производную (по h) функции g(h). Таким образом, имеем: 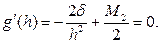 Откуда получаем формулу для оптимального шага:
Откуда получаем формулу для оптимального шага:
hопт = 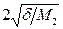 (56)
(56)
Из формулы (56) видно, что сделать аппроксимацию производной в точке xi приближённым разностным отношением (54) сколь угодно качественной можно лишь в том случае, когда величину d можно сделать сколь угодно малой (что возможно лишь при очень точном задании функции f (xi) таблицей её значений yi). Тогда можно рассчитывать на малость hопт, что в свою очередь, обеспечит малость
gмин = g(hопт).
Примеры решения типовых задач.
Пример 1.
Найти y¢(50) для функции y = 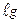 (x), заданной таблицей 1:
(x), заданной таблицей 1:
Таблица 1 – значения функции y = 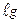 (x).
(x).
| i | xi | yi | Dyi | D2yi | D3yi |
| 1.6990 1.7404 1.7782 1.8129 | 0.0414 0.0378 0.0347 | - 0.0036 - 0.0031 | 0.0005 |
Дополняем таблицу значений функции значениями конечных разностей. Из таблицы видно, что h = 5. Для решения задачи воспользуемся формулой (11), выбирая в качестве базового узла значение xi = 50:
y¢(xi) @ 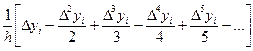
Выбирая из таблицы (1) имеющиеся в нашем распоряжении значения конечных разностей Dyi, D2yi, D3yi получим:
y¢(50) @ 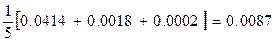 ,
,
Для оценки точности найденного значения производной воспользуемся формулой y = 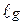 (x) = 0.43429
(x) = 0.43429 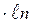 (x), поэтому y¢(x) = 0.43429
(x), поэтому y¢(x) = 0.43429 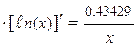 , следовательно, получаем y¢ (50) =
, следовательно, получаем y¢ (50) = 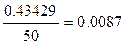 . Таким образом, результаты совпадают с точностью до четвёртого знака.
. Таким образом, результаты совпадают с точностью до четвёртого знака.
Пример 2.
Бесконечно гладкая функция y = f (x) задана таблицей своих значений и значений конечных разностей (табл. 2). Найти приближения к значению f¢ (1.5), пользуясь простейшими аппроксимациями по формулам первого и второго порядка точности.
Таблица - 2Значения бесконечно гладкой функции и её конечных разностей
| x | y | Dy | D2y | D3y | D4y | D5y |
| 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 | 0.367879 0.332871 0.301194 0.272532 0.246597 0.223130 0.201897 0.182684 0.165299 0.149569 0.135335 | - 0.035008 - 0.031677 - 0.028662 - 0.025935 - 0.023467 - 0.021233 - 0.019213 - 0.017385 - 0.015730 - 0.014234 | 0.003331 0.003015 0.002727 0.002468 0.002234 0.002020 0.001828 0.001655 0.001496 | - 0.000316 - 0.000288 - 0.000259 - 0.000234 - 0.000214 - 0.000192 - 0.000173 - 0.000159 | 0.000028 0.000029 0.000025 0.000020 0.000022 0.000019 0.000014 | 0.000001 - 0.000004 - 0.000005 0.000002 - 0.000003 - 0.000005 |
Для решения задачи нам понадобятся следующие формулы:
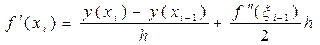 , x i– 1 Î(x i– 1; xi). (27)
, x i– 1 Î(x i– 1; xi). (27)
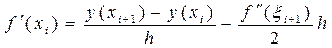 , x i+1 Î(x i; xi+1) (28)
, x i+1 Î(x i; xi+1) (28)
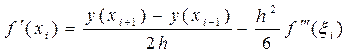 , x iÎ( x i-1; x i+1). (33)
, x iÎ( x i-1; x i+1). (33)
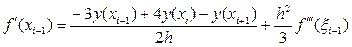 , xi-1Î(x i-1, x i+1) (50)
, xi-1Î(x i-1, x i+1) (50)
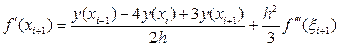 , xi+1Î(x i-1, x i+1) (51)
, xi+1Î(x i-1, x i+1) (51)
Выбрав xi–1 = 1.4, yi–1 = 0.246597; xi = 1.5, yi = 0.223130; xi+1 = 1.6, yi+1 = 0.201897; получим:
По формуле (27): 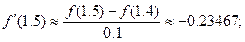 (57)
(57)
По формуле (28): 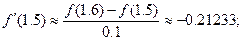 (58)
(58)
По формуле (33): 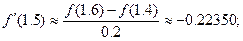 (59)
(59)
По формуле (50): 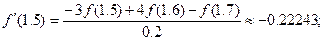 (60)
(60)
По формуле (51): 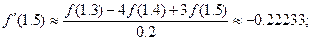 (61)
(61)
Оценим погрешности полученных значений для f¢ (1.5).
Формулы (57), (58). Для значений f¢ (1.5), полученных по формулам (57), (58) ошибка аппроксимации производной определяется соответственно выражениями:
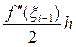 , x i–1 Î(x i–1; xi) и
, x i–1 Î(x i–1; xi) и 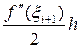 , x i+1 Î(x i; xi+1) .
, x i+1 Î(x i; xi+1) .
Формула (57). Заменяя на участке (x i–1; xi) = (1.4; 1.5) производную 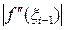 выражением
выражением 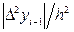 получим:
получим: 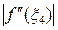 =
= 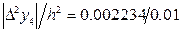 , поэтому величина погрешности
, поэтому величина погрешности 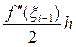 для значения – 0.23467 составляет
для значения – 0.23467 составляет 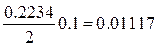 .
.
Формула (58). Заменяя на участке (x i; xi+1) = (1.5; 1.6) производную 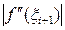 выражением
выражением 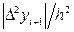 получим:
получим: 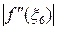 =
= 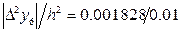 , поэтому величина погрешности
, поэтому величина погрешности 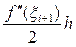 для значения – 0.21233 составляет
для значения – 0.21233 составляет 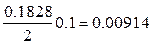 .
.
Формула (59). Для значения f¢ (1.5), полученного по формуле (59), ошибка аппроксимации производной определяется выражением:
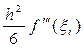 , x iÎ( x i–1; x i+1).
, x iÎ( x i–1; x i+1).
Заменяя на участке (x i–1; xi+1) = (1.4; 1.6) производную 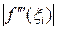 выражением max
выражением max 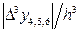 получим:
получим: 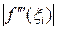 =
= 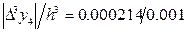 , поэтому величина погрешности
, поэтому величина погрешности 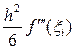 для значения f¢ (1.5) = – 0.22350 составляет
для значения f¢ (1.5) = – 0.22350 составляет 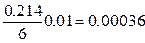 .
.
Формулы (60), (61). Для значений f¢ (1.5), полученных по формулам (60), (61) ошибка аппроксимации производной определяется соответственно выражениями:
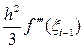 , xi-1Î(x i-1, x i) и
, xi-1Î(x i-1, x i) и 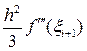 , xi+1Î(x i, x i+1)
, xi+1Î(x i, x i+1)
аналогично тому, как это было сделано в предыдущих примерах.
Заключение (аннотация к лекции №21 – численное дифференцирование).
В лекции №21 рассмотрена постановка задачи численного дифференцирования, приведена графическая иллюстрация операции численного дифференцирования. Отмечено, что в рамках разработанных подходов приближённое дифференцирование представляет собой операцию «менее точную», чем рассмотренное ранее приближённое интегрирование.
Формулы численного дифференцирования получены в рамках двух наиболее часто используемых на практике подходов – представление дифференцируемой функции интерполяционным полиномом или её разложение в ряд Тейлора.
Дан вывод конечноразностных формул численного дифференцирования основанный на замене дифференцируемой функции интерполирующим её полиномом Ньютона с последующим дифференцированием полученных выражений. Приведены формулы для вычисления приближённых значений производных функции в узловых точках таблицы. Даны практические рекомендации по использованию конечноразностных формул численного дифференцирования.
Полученные конечноразностные формулы численного дифференцирования адаптированы для наиболее часто используемых практических ситуаций (случай линейной интерполяции по двум точкам, случай квадратичной интерполяции по трём точкам, случай кубической интерполяции по четырём точкам).
В рамках подхода на основе формулы Тейлора получены наиболее часто востребованные на практике аппроксимации производных в виде разностных отношений различного порядка точности:
для аппроксимации первой производной получены:
– формула несимметричной аппроксимации f¢ (x) первого порядка точности;
– формула симметричной аппроксимации f¢ (x) второго порядка точности.
для аппроксимации второй производной получены:
– формула симметричной аппроксимации f¢¢ (x) второго порядка точности.
– формула несимметричной аппроксимации f¢¢ (x) первого порядка точности.
Получено выражение для оценки погрешности формул численного дифференцирования в узловых точках таблицы значений функции.
Рассмотрен вопрос по оптимизации шага численного дифференцирования при ограниченной точности задания значений функции.
Приведены примеры решения типовых задач.
Литература:
1. Б.П. Демидович и И.А. Марон. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.
2. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 с.
3. Г.М. Фихтенгольц. Основы математического анализа, том 1. – М.: Наука, 1968. – 440 с.
Вопросы по теме
«Численное дифференцирование»
( Лекция 4 )
1. Постановка задачи численного дифференцирования. Подход к процедуре численного дифференцирования и определению погрешности аппроксимации производной. Геометрическая иллюстрация задачи численного дифференцирования.
2. Конечноразностные формулы численного дифференцирования. Формулы численного дифференцирования на основе первой интерполяционной формулы Ньютона. Численное дифференцирование в узловых точках таблицы. Практические рекомендации использования формул численного дифференцирования.
3. Связь приближённых значений производной функции с узловыми значениями самой функции - случаи линейной, квадратичной и кубической интерполяции.
4. Формулы аппроксимации для первой производной и характеристика их точности: формула первого порядка точности для f¢ (x) - случай простой несимметричной аппроксимации; формула второго порядка точности для f¢ (x) - случай простой симметричной аппроксимации.
5. Формулы аппроксимации для второй производной f¢¢ (x) и характеристика их точности: симметричная аппроксимация f¢¢ (x) второго порядка точности; несимметричная аппроксимация f¢¢ (x) первого порядка точности.
6. Выражения для погрешности формул численного дифференцирования:получение формулы для ошибки аппроксимации первой производной на основе дифференцирования выражения для ошибки интерполяционной формулы Ньютона.
7. Оптимизация шага численного дифференцирования при ограниченной точности значений функции. Анализ составляющих полной абсолютной погрешности аппроксимации производной первого порядка на примере аппроксимации первой производной f¢ (x) несимметричным разностным отношением. Понятие оптимального шага сетки (таблицы представления данных), минимизирующего погрешность аппроксимации производной.
Дата добавления: 2015-09-14; просмотров: 4138;
