ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
 Вернемся к рассмотрению двух инерциальных систем отчета
Вернемся к рассмотрению двух инерциальных систем отчета 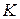 и
и 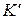 , которые мы ввели при рассмотрении преобразований Галилея. Напомним, что оси
, которые мы ввели при рассмотрении преобразований Галилея. Напомним, что оси 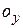 и
и 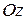 системы
системы 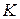 параллельны соответствующим осям
параллельны соответствующим осям 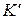 , оси
, оси 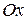 и
и 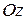 системы
системы 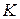 параллельны соответствующим осям
параллельны соответствующим осям 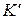 , оси
, оси 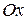 и
и 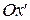 совпадают по направлению, система
совпадают по направлению, система 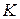 движется со скоростью
движется со скоростью 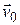 , направленной вдоль оси
, направленной вдоль оси 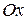 , относительно
, относительно 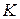 , которая.
, которая.
Из преобразований Галилея следует закон сложения скоростей, согласно которому 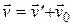 . Применим этот закон к распространению света. Если в системе
. Применим этот закон к распространению света. Если в системе 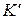 вдоль оси
вдоль оси 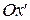 распространяется световой сигнал со скоростью с, то в системе
распространяется световой сигнал со скоростью с, то в системе 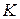 его скорость должна быть
его скорость должна быть 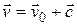 . Но это противоречит принципу постоянства скорости света с. Следовательно, преобразования Галилея должны быть заменены другими формулами.
. Но это противоречит принципу постоянства скорости света с. Следовательно, преобразования Галилея должны быть заменены другими формулами.
Формулы преобразований координат, согласующиеся с принципом постоянства скорости света, нашел Лоренц. Эти формулы называются преобразованиями Лоренца и имеют вид:
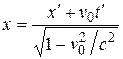 ;
; 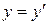 ;
; 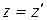 ;
; 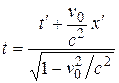 . (6.1)
. (6.1)
Часто встречающееся отношение 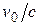 бывает удобно заманить общепринятым обозначением
бывает удобно заманить общепринятым обозначением 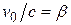 . В этом случае преобразования Лоренца (6.1) приобретают вид:
. В этом случае преобразования Лоренца (6.1) приобретают вид:
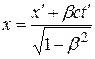 ;
; 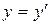 ;
; 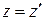 ;
; 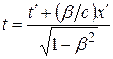 (6.2)
(6.2)
Обратный переход к координатам системы 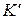 совершается по формулам:
совершается по формулам:
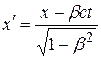 ; ;
; ; 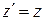 ;
; 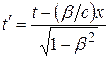 (6.3)
(6.3)
Необходимо подчеркнуть две особенности формул преобразований Лоренца. С одной стороны, пространственные координаты и время оказываются взаимосвязанными и рассматриваются в теории относительности как единое четырехмерное пространство-время.
С другой стороны, формулы преобразований Лоренца теряют смысл, если 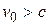 .Эта ихособенность математически отражает тот факт, что скорость движения света в пустоте является предельной скоростью распространения взаимодействий в пространстве. Со скоростью света могут двигаться только особые частицы, такие, как фотоны, обладающие нулевой массой покоя. Для обычных, окружающих нас тел, движение со скоростью
.Эта ихособенность математически отражает тот факт, что скорость движения света в пустоте является предельной скоростью распространения взаимодействий в пространстве. Со скоростью света могут двигаться только особые частицы, такие, как фотоны, обладающие нулевой массой покоя. Для обычных, окружающих нас тел, движение со скоростью 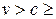 невозможно.
невозможно.
Дата добавления: 2015-09-14; просмотров: 1082;
