И ФАЗЫ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Как видно из (5.42), амплитуда вынужденных колебаний зависит от частоты и при некоторой частоте достигает максимума. Эта частота называется резонансной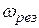 
, а само явление резонансом.
Максимуму амплитуды соответствует минимум знаменателя (5.40), поэтому производная от выражения в знаменателе (5.40) должна быть равна нулю:
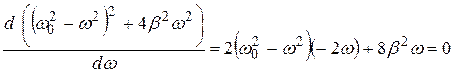. (5.43)
Уравнение (5.43) имеет три решения: 
, 
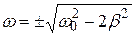. Нулевое и отрицательное значение 
не имеют физического смысла, а значит резонансная частота
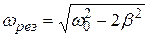. (5.44)
Подставив это значение частоты в выражение в (5.40), найдем значение амплитуды при резонансе:
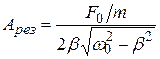. (5.45)
Зависимость амплитуды колебаний от частоты внешнего воздействия называют резонансной кривой или резонансной характеристикой.
Примерный вид резонансных характеристик колебательной системы, в которой изменяют затухание, показан на рисунке 5.8.
Если в системе отсутствует затухание, т.е. коэффициент затухания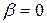 
, то резонансная амплитуд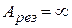а 
, а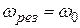 
. На рисунке этому условию соответствует кривая 1. Практически такая ситуация не реализуется, но чем меньше затухание, тем ближе резонансная кривая к этому идеальному случаю.
С увеличением затухания резонансная амплитуда уменьшается, резонансная частота в соответствии с (5.43) также уменьшается. Поэтому максимум резонансной кривой становится ниже и смещается влево (кривые 2, 3, 4).
Резонансные характеристики несимметричны: если частота вынуждающей силы стремится к нулю, то все резонансные кривые стремятся к одинаковому значению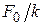 
, соответствующему смещению системы из положения равновесия под действием постоянной силы. При возрастании частоты вынуждающей силы все резонансные кривые стремятся к нулю. Это означает, что под действием быстропеременной силы система не успевает заметно сместиться из положения равновесия и амплитуда колебаний становится незначительной. (Вспомните раскачивание качелей… Приложив постоянную силу определенной величины, мы получим некоторое смещение из положения равновесия. Если с такой же по амплитуде силой пытаться раскачивать качели на максимально доступной частоте – отклонение от положения равновесия будет совсем незначительным.)
Зависимость сдвига фаз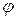 
между периодическим внешним воздействием и колебаниями, совершаемыми системой, называют фазовой характеристикой системы.
Вынужденные колебания отстают по фазе от вынуждающей силы. Примерный вид этой зависимости показан рисунке 5.8. Отметим, что независимо от затухания в системе сдвиг по фазе достигает значение 
при частоте, равной собственной частоте колебаний системы. Следовательно, эта зависимость может быть использована для определения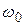 
.
Дата добавления: 2015-09-14; просмотров: 957;