КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПРИ ПЛОСКОМ ДВИЖЕНИИ

Рассмотрим, как вычислить кинетическую энергию тела, если оно одновременно участвует в поступательном и вращательном движении – например, качение колеса по плоскости.

Как мы знаем, при плоском движении тела скорость некоторой точки тела определяется формулой

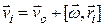(4.26)

где 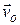- скорость поступательного движения точки «0», принятой за начало отсчета для ,

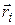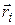- радиус-вектор частицы с массой 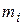по отношению к точке «0». Тогда кинетическая энергия i-той частицы

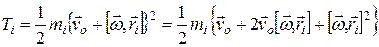(4.27)

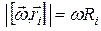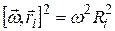Учтем, что модуль , - расстояние i-той точки до оси вращения и, соответственно . Воспользовавшись циклической перестановкой сомножителей в смешенном произведении, получим .

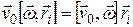Тогда из (4.27) получим:

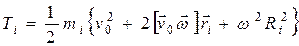(4.28)

А для кинетической энергии всего тела

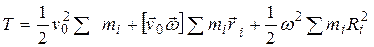(4.29)

Теперь учтем, что

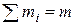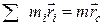, , а .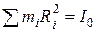

Тогда

(4.30)

Если в качестве «0» взять центр масс, то 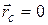, и

(4.31)

Таким образом, если рассматривать вращение тела относительно оси, проходящей через центр масс, то его кинетическая энергия распадается на два слагаемых. Одно из них описывает кинетическую энергию, обусловленную поступательным движением, другое – вращательным.