МОМЕНТ ИНЕРЦИИ
Момент инерции, аналогично массе тела, в соответствии с его определением (4.11) является величиной аддитивной и может считаться характеристикой тела, независимо от того, вращается оно или нет.
В значительной степени момент инерции зависит от распределения массы в пределах тела, которое характеризуют плотностью тела:
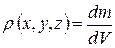 (4.17)
(4.17)
Под 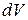 в (4.17) понимается физически бесконечно малый объем, т.е. настолько малый, что все макроскопические свойства в его пределах можно считать постоянным, но достаточно большой, чтобы не проявлялась дискретностью строения вещества.
в (4.17) понимается физически бесконечно малый объем, т.е. настолько малый, что все макроскопические свойства в его пределах можно считать постоянным, но достаточно большой, чтобы не проявлялась дискретностью строения вещества.
Соответственно, точная формула для вычисления 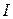 получается из (4.11) и имеет вид:
получается из (4.11) и имеет вид:
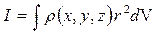 . (4.18)
. (4.18)
По сравнению с (4.11) в (4.18) 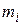 заменены на бесконечно малые
заменены на бесконечно малые 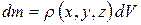 , находящиеся от оси вращения на расстоянии
, находящиеся от оси вращения на расстоянии 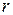 .
.
 В качестве примера использования формулы (4.18) рассмотрим вычисление момента инерции однородного диска радиуса
В качестве примера использования формулы (4.18) рассмотрим вычисление момента инерции однородного диска радиуса 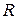 относительно оси, перпендикулярной к его плоскости и проходящей через его центр. Разобьем мысленно диск (рисунок 4.5.) на кольцевые слои с радиусом
относительно оси, перпендикулярной к его плоскости и проходящей через его центр. Разобьем мысленно диск (рисунок 4.5.) на кольцевые слои с радиусом 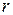 и толщиной
и толщиной 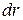 , толщина диска равна b. Объем кольцевого слоя
, толщина диска равна b. Объем кольцевого слоя
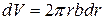 (4.19)
(4.19)
Его масса 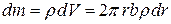 . Все точки кольцевого слоя находятся на одинаковом расстоянии
. Все точки кольцевого слоя находятся на одинаковом расстоянии 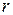 от оси вращения, поэтому его момент инерции
от оси вращения, поэтому его момент инерции
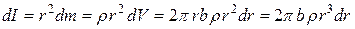 . (4.20)
. (4.20)
Момент инерции всего диска равен сумме моментов инерции кольцевых слоев:
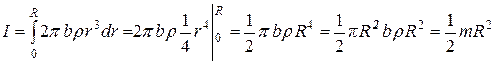 . (4.21)
. (4.21)
 |
Аналогично можно рассчитать моменты других тел с правильной геометрической формой. Для шара:
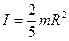 , для тонкого однородного стержня длинной
, для тонкого однородного стержня длинной 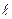 :
:
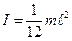 , для тонкого диска, относительно оси, лежащей в его плоскости и проходящей через центр:
, для тонкого диска, относительно оси, лежащей в его плоскости и проходящей через центр: 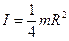 .
.
 |
Вычисление моментов инерции для тел сложной формы значительно облегчается при использовании теоремы Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции
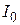 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями d:
относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями d: 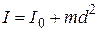 .
.
Например, при вращении сложного тела, по форме напоминающего гантель (рисунок 4.7) вокруг оси «ОО» проходящей через центр одного из шаров, его момент инерции можно представить состоящим из трех составляющих: момента инерции левого шара, стержня и правого шара. Последние в свою очередь по теореме Штейнера состоят из двух частей – момента инерции относительно оси проходящей через центр масс и произведения массы соответствующего тела на квадрат расстояния между осями.
Дата добавления: 2015-09-14; просмотров: 1219;
