ДВИЖЕНИЕ ЦЕНТРА МАСС ТВЕРДОГО ТЕЛА
Твердое тело можно представить как систему 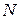 жестко связанных материальных точек массой
жестко связанных материальных точек массой 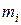 . На каждую из частиц действуют внутренние силы со стороны других частиц, образующих тело, а также внешние силы. Поэтому уравнение движения для
. На каждую из частиц действуют внутренние силы со стороны других частиц, образующих тело, а также внешние силы. Поэтому уравнение движения для 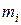 имеет вид:
имеет вид:
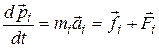 (4.1)
(4.1)
где 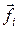 – результирующая сила всех внутренних сил, действующих на
– результирующая сила всех внутренних сил, действующих на 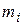 ,
,
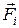 – результирующая сила всех внешних сил, действующих на
– результирующая сила всех внешних сил, действующих на 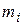 .
.
Для каждой 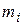 справедливо уравнение вида (4.1), и всего можно записать
справедливо уравнение вида (4.1), и всего можно записать 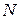 таких уравнений. Суммируя левые и правые части уравнений, получим:
таких уравнений. Суммируя левые и правые части уравнений, получим:
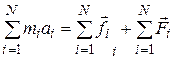 (4.2)
(4.2)
Сумма внутренних сил, как мы знаем, равна нулю. Из определения центра инерции следует:
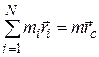 . (4.3)
. (4.3)
где 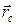 – радиус-вектор центра масс системы,
– радиус-вектор центра масс системы,
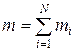 – масса всей системы.
– масса всей системы.
Дифференцируя соотношение (4.3) дважды по времени, найдем, в соответствии с определением ускорения,
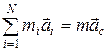 (4.4)
(4.4)
Сравнивая соотношения (4.2) и (4.4), получаем:
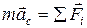 . (4.5) Уравнение (4.5) соответствует уравнению движения материальной точки с массой
. (4.5) Уравнение (4.5) соответствует уравнению движения материальной точки с массой 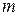 под действием всех внешних сил. Поэтому приходим к важному выводу: центр инерции твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела под действием всех приложенных к телу сил.
под действием всех внешних сил. Поэтому приходим к важному выводу: центр инерции твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела под действием всех приложенных к телу сил.
Дата добавления: 2015-09-14; просмотров: 885;
