ЦЕНТР МАСС И ЕГО ДВИЖЕНИЕ

Вторым аддитивным интегралом движения, сохраняющимся для замкнутой системы является её импульс.

Рассмотрим систему 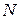взаимодействующих частиц. На i-тую частицу системы действуют внутренние силы 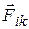и внешне с результирующей 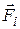. Уравнение движения i-той частицы имеет вид:

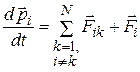(3.57)

Аналогичные уравнения, очевидно можно записать для каждой из 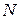частиц. Сложив левые и правые части уравнений, получим

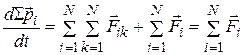(3.58)

Двойная сумма в (3.58) представляет собой сумму всех внутренних сил системы. По третьему закону Ньютона 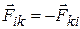, и для каждого слагаемого в этой сумме найдется противоположный ему вектор. Поэтому .

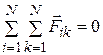По определению импульсом системы называютвекторную сумму импульсов тел системы, т.е. величину 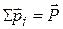. Таким образом, в левой части (3.58) стоит производная импульса системы. Если система замкнута, то из (3.58) следует, что

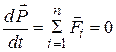(3.58)

Таким образом, импульс замкнутой системы материальных точек остается постоянным. Это утверждение называют законом сохранения импульса.

Требование отсутствия внешних сил не является жестким. Если в пространстве существует такое направление, что проекция суммы результирующих внешних сил на него равна нулю, то, в соответствии с (3.58), проекция импульса системы на это направление будет оставаться постоянной.

Важным свойством обладает точка, называемая центром масс системы. Если система образована материальными точками с массами 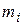, а их положение задается радиус-векторами 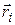, то по определению центром масс называется точка, положение которой задается радиус-вектором 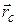, определяемым следующим выражением:

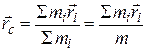(3.59)

где 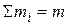есть масса всей системы.

Взяв производную от выражения (48), получим скорость центра инерции:

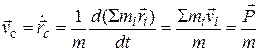(3.60)

Как видно из (3.60) импульс системы

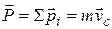(3.61)

равен произведению ее массы на скорость центра инерции.

Кроме того, соотношение (3.58) позволяет утверждать, что если система замкнута, то ее центр масс движется равномерно и прямолинейно или покоится.

3.13. СОУДАРЕНИЕ ДВУХ ТЕЛ – самостоятельно.