МАЛЫЕ КОЛЕБАНИЯ ПРОИЗВОЛЬНОЙ СИСТЕМЫ.

Для упрощения рассуждений ограничимся рассмотрением одномерного случая и рассмотрим систему, положение которой может быть задано с помощью одной координаты 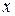. Можно представить себе шарик (материальную точку), который катится по желобу. Желоб расположен в одной плоскости, а его высота изменяется при движении шарика. Потенциальная энергия шарика в поле силы тяжести будет тогда функцией одной переменной, определяющей положения шарика в желобе. Соответственно потенциальная энергия системы будет функцией одной переменной: 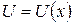. В первом приближении будем считать, что силы сопротивления движению шарика отсутствуют.

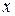Рассмотрим ситуацию вблизи положения устойчивого равновесия. Будем отсчитывать от положения равновесия. Разложим 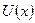в ряд в окрестности положения равновесия и ограничимся рассмотрением малых колебаний, т.е. малыми значениями 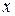. В этом случае членами с высшими степенями 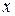в разложении 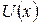можно пренебречь и считать, что в окрестности точки с координатой :

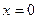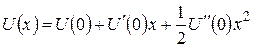(5.1)

(отметим, что определение малых колебаний фактически в том и заключается, что при совершении колебаний система отклоняется от положения равновесия настолько мало, что зависимость ее потенциальной энергии от координаты с достаточной, в рассматриваемой задаче, точностью выражается соотношением (5.1).)

Вследствие того, что потенциальная энергия системы определена с точностью до произвольной константы, примем, что в положении равновесия она равна нулю: 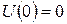. Поэтому первое слагаемое в разложении можно отбросить.

В положении устойчивого равновесия потенциальная энергия имеет минимум. Поэтому первая производная должна быть равна нулю в точке равновесия: 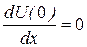(условие экстремума), а вторая положительна: 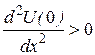(условие минимума). Обозначим 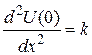. Тогда зависимость потенциальной энергии от координаты можно представить в виде:

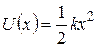(5.2)

Обратите внимание на то, что соотношение (5.2) аналогично выражению для потенциальной энергии деформированной пружины. Соответственно сила, действующая на систему, описывается формулой:

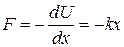. (5.3)

Очевидно, что формула (5.3) аналогично закону Гука, поэтому силы, описываемые соотношением типа (5.3), независимо от их природы называют квазиупругими.

Единственное ограничение, которое мы сделали при получении соотношения (5.3) заключалось в предположении о малости отклонений от положения равновесия. Даже вид функции 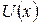не имеет значения – достаточно чтобы в окрестности точки рассмотрения у нее был минимум. Таким образом, любая механическая система при малом отклонении от положения устойчивого равновесия находится под воздействием квазиупругой силы.

Рассмотрим движение системы под действием только квазиупругой силы (считаем, что силы сопротивления движению отсутствуют!). Если масса системы равна 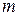, то уравнение движения системы имеет вид:

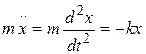. (5.4)

Разделив уравнение (5.4) на 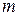, получим

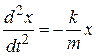или

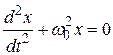(5.5)

где использовано обозначение .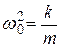

Итак, если система находится под воздействием только квазиупругой силы, то ее движение описывается дифференциальным уравнением (5.5).

Таким уравнением описывается движение шарика на рисунке 5.1, груза, подвешенного на пружине, маятников и многих других систем. Для всех таких систем существует общее название: гармонический осциллятор. Название связано с тем, что такие системы совершают простейшие, гармонические колебания. Немного ниже мы рассмотрим этот вопрос подробней.

Вполне очевидно, что гармонический осциллятор представляет собой абсолютную идеализацию и в чистом виде не встречается. Во всякой реальной колебательной системе обязательно действуют силы 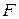сопротивления, которые приводят к диссипации механической энергии системы, причем чаще всего сила сопротивления оказывается пропорциональной скорости:

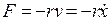(5.6)

В этом случае в уравнение движения необходимо добавить силу сопротивления, и оно принимает вид:

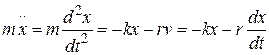. (5.7)

Тогда дифференциальное уравнение, описывающее движение в этом случае, будет иметь вид:

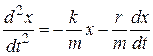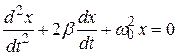или (5.8)

где .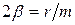

Если на систему кроме квазиупругой действуют диссипативные силы, то она совершает свободные колебания. Таким образом, свободные колебания системы описываются дифференциальным уравнением (5.8).

Очень часто встречаются ситуации, когда система совершает вынужденные колебания под действием внешней периодической силы. В простейшем случае внешняя сила изменяется по закону 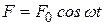. Уравнение движения в этом случае примет следующий вид:

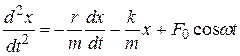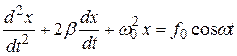или (5.9)

где .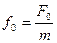

Уравнения (5.5), (5.8) и (5.9) являются линейными дифференцированными уравнениями с постоянными коэффициентами. Для их решения в математике разработан специальный метод, который изложен не только в учебниках по математике, но и во многих учебниках по физике. Изучить (или вспомнить) методику решения линейных дифференциальных уравнений этого вида необходимо самостоятельно.