ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ.

Рассмотрим решение уравнения (5.5). Следуя известной технологии решения линейных дифференциальных уравнений, предположим, что решение уравнения (5.5) имеет вид 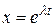. Подставив в уравнение это решение, получим характеристическоеуравнение:

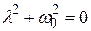, (5.10)

два корня, которого равны

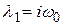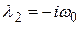; . (5.11)

Тогда общее решение уравнения (5.5) имеет вид:

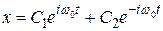(5.12)

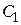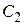где и - комплексные константы, которые нам необходимо найти.

Воспользуемся тем, что функция, описывающая колебания реальной физической системы, должна быть вещественной, а значит, комплексно сопряженное выражение для смещения из положения равновесия должно совпадать с самим выражением: 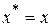, т.е.

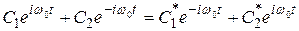(5.13)

Для выполнения соотношения (5.13) необходимо, чтобы были равны коэффициенты слева и справа перед выражениям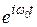и и :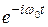

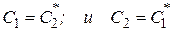. (5.14)

Представим комплексные числа 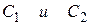в экспоненциальном виде (в показательной форме), а чтобы выполнялось условие (5.14) положим:

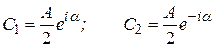(5.15)

где и 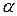- произвольные константы.

Фактически мы заменяем произвольные константы 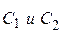на (также произволдьные) и 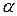. Однако это представление оказывается более удобным.

При этих значениях констант 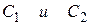получаем (подставив (5.15) в (5.12):

.

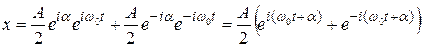Преобразуем это соотношение по формуле Эйлера: для любого вещественного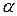

.

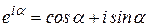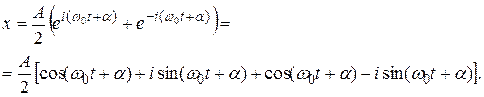(5.16)

Таким образом,

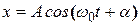(5.17)

Отметим, что произвольные константы и 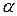можно выбрать так, чтобы 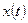изменился по закону .

Таким образом, если система находится под действием только квазиупругой силы, то ее смещение из положения равновесия изменяется по закону

sin(ωt + α) или cos(ωt + α), т.е. система совершает гармонические колебания.

Вспомнимопределения:

§ - максимальное отклонение от положения равновесия называют амплитудой колебания,

§ величину - текущей фразой колебания,

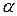§ - начальной фазой колебания,

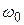§ - круговой (циклической) частотой,(рад/с),

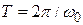§ - промежуток времени, через который движение системы повторяется, называют периодом колебания,

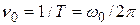§ - частотой (Гц).

Рассмотрим как изменяются в процессе колебаний скорость и ускорение колеблющегося тела. Взяв от (5.17) производную по времени, получим уравнение, описывающее колебания скорости системы:

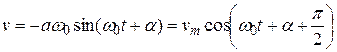
Очевидно, что колебания скорости происходят с амплитудой 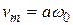, а текущая фаза колебаний на 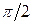больше, т.е. по фазе колебания скорости опережают колебания смещения на .

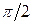Производная по времени от скорости дает зависимость ускорения от времени:

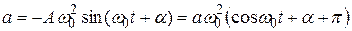. (5.18)

Очевидно, что изменение во времени ускорения на 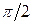опережает скорость, а смещение из положение равновесия - на 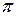. Это означает, что смещение и ускорение при гармонических колебаниях изменяются в противофазе.

Каждое конкретное колебание, которое может совершать система, характеризуется определенными значениями амплитуды и фазы 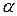. Эти значения могут быть определены по начальным условиям, т.е. по значениям смещения 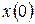и скорости 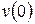системы в момент времени 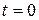. Для примера представим две ситуации. В первой маятник отклоняют от положения равновесия и в момент начала отсчета времени отпускают. В этом случае колебания будут описываться уравнением вида 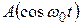. Если мысленно сместить начало отсчета времени на момент, когда маятник проходит положение равновесия, уравнение колебаний будет иметь вид .

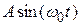Колебания, которые совершает система под действием только квази­упругой силы называются собствен­ными колебаниями. Отличительной особенностью собственных колебаний являются их гармонический характер, который подразумевает абсолютное постоянство амплитуды, частоты и фазы колебаний, причем частота колебаний определяется соотношением (5.5).