Кусочно-линейные агрегаты

Как показывает анализ моделирующих алгоритмов, можно добиться их су­щес­твенных упрощений, если рассматривать объекты более частные, чем агрегат общего вида, но сохраняющие возможность описания достаточно широкого класса реальных систем. Пра­ктически удобным для формализации широкой сово­куп­но­сти разнообразных процессов и явлений материального мира являются так называемые кусочно-линейные агрегаты (КЛА).

Понятие о кусочно-линейном агрегате.Для поставленных здесь задач достаточно считать, что на агрегат не посту­па­ют управляющие сигналы z, а поступают лишь входные сигналы u(это допущение не огра­ни­чивает общности, так как в качестве u можно рассматривать входной сигнал в ши­ро­ком смысле, в том числе и управляющий). Итак, мы рассматриваем агрегат как объект, который в каж­дый момент времени t характеризуется внутренним состоянием x(t), имеет вход и выход. На вход агрегат в изолированные моменты времени могут пос­ту­пать сигналы, с выхода могут сниматься выходные сигналы. Класс кусоч­но-линейных агрегатов выделяется с помощью конкретизации структуры множеств X, U, Y а также операторов H и G, которые представляют собой линейные пространства. Опишем данную конкретизацию.

Рассмотрим некоторое конечное или счетное множество I. Для определенности предположим, что I = {0,1,2,…}, хотя в конкретных задачах I может иметь и другой вид. НазовемI множеством особых состояний, а элементы nÎI – особыми состояниями. Каждому особому состоянию nÎI поставим в соответствие некоторое целое неотрицательное число ||n||, которое назовем рангом основного состояния (смысл этой величины – размерность вектора n-го состояния). Кроме того, каждому nÎI поставим в соответствие выпуклый многогранник X⁽ⁿ⁾ (множество допустимых значений для состояния n) в евклидовом пространстве размерности ||n||. Будем считать, что X = ÈX⁽ⁿ⁾, т. е. пространство состояний X можно представить состоящим из всевозможных пар вида ( 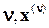), где nÎI, а x⁽ⁿ⁾ является вектором размерности ||n|| и принимает значения из многогранника X⁽ⁿ⁾. Вектор x⁽ⁿ⁾ будем называть вектором координат. Если ||n|| = 0 для некоторого n, то это означает, что в данном состоянии n координаты не определяются.

В виде КЛА могут быть формализованы многие реальные процессы: процессы передачи и обмена данными в сетях связи, системы массового обслуживания и материально-технического снаб­же­­­ния, процессы автомо­биль­ного движения на дорогах, разнообразные дис­к­рет­ные производ­ст­венные процессы, вычислительные системы и т.д. При этом всюду основные состояния агрегата указывают на качественно различ­ные состояния модели­руемых объектов. Дополнительные же координаты ха­ра­к­теризуют происхо­дящие количественные изменения и часто носят сугубо вспомогательный характер, «вбирая» в себя необходимую инфор­ма­цию о пре­дыстории модели. Следует отметить, что представление реальных систем в форме КЛА неоднозначно, поскольку неоднозначно могут быть выбраны сос­тояния агрегатов. Выбор же состояний определяется как целями иссле­дования, так и стремлением уменьшить размерность задачи. При этом всегда приходится идти на компромисс между точностью описания и полнотой получаемой информации с одной стороны и простотой модели – с другой.