Я количественная мера информации

I=mⁿ(3.1)

Недостаток этой меры – неадитивность (непропорциональность количества информации и длины сообщения). Логично предположить, что сообщение, имеющее, например, в два раза большую длину, несет в два раза большую информацию.

2-я количественная мера – мера Р.Хартли

Роберт Хартли – американский инженер, работал в телеграфной компании. Рассуждая о количестве информации, содержащемся в телеграфном тексте, заложил основы те­о­рии информации, определив логарифмическую меру количества информации (1928г.).

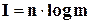(3.2)

Отсюда возникла и двоичная единица информации. Сообщение должно иметь минимум один символ: n_min=1. Алфавит должен иметь минимум два элемента: m_min=2. Вот в таком сообщении и содержится минимально возможное количество информации.

I_min = n_min∙log m_min

При использовании двоичного логарифма I_min = 1 (бит, от англ. binary digit).Поэтому в теории информации используется логарифм по основанию 2.

I = n∙log₂m.(3.3)

Мера Хартли (логарифмическая мера) (3.2) не учитывает вероятностный характер сообщения (вспомним, что сообщение имеет смысл, когда оно неизвестно заранее).

3-я количественная мера – мера К.Шеннона

Количественная мера Шеннона получена из следующих соображений. Если символ появляется в сообщении с вероятностью 1 (на определенном месте), то такой символ никакой информации не несет. В случае если любой из m символов алфавита равновероятен p=1/m. Количество информации, содержащееся в сообщении из одного элемента определяется так: