Пример решения задания №3

Исходные данные:

Кодовая комбинация двоичного кода, соответствующая команде 1 (табл. 3.10):

х₇ х₆ х₅ х₄ х₃ х₂ х₁ х₀

1 0 0 0 0 0 0 0

Кодовая комбинация двоичного кода, соответствующая команде 2 (табл. 3.10):

х₇ х₆ х₅ х₄ х₃ х₂ х₁ х₀

1 1 1 1 1 1 1 0

Вероятность передачи команды 1: р_п1 = 0,8.

Вероятность передачи команды 2: р_п2 = 0,2.

Вероятность правильного приема каждого символа кодовой комбинации: р_с = 0,6.

Определяем значение принятой кодовой комбинации путем представления значения заданного варианта в виде суммы степеней числа 2, начиная с ближайшего меньшего числа: 130 = 128 + 2 = 2⁷ + 2¹. Степени числа 2 показывают индекс двоичного числа, равного 1:

у₇ у₆ у₅ у₄ у₃ у₂ у₁ у₀

1 0 0 0 0 0 1 0

Если двоичное представление заданного варианта имеет меньшее число разрядов (например, 055 = 32 + 16 + 4 + 2 + 1 = 2⁵ + 2⁴ + 2² + 2¹ + 2⁰):

у₇ у₆ у₅ у₄ у₃ у₂ у₁ у₀

1 1 0 1 1 1,

то слева необходимо по выбору студента произвольно проставить значения недостающих символов:

у₇ у₆ у₅ у₄ у₃ у₂ у₁ у₀

0 0 1 1 0 1 1 1 , или

у₇ у₆ у₅ у₄ у₃ у₂ у₁ у₀

0 1 1 1 0 1 1 1 , или

у₇ у₆ у₅ у₄ у₃ у₂ у₁ у₀

1 0 1 1 0 1 1 1 , или

у₇ у₆ у₅ у₄ у₃ у₂ у₁ у₀

1 1 1 1 0 1 1 1 .

Если двоичное представление заданного варианта имеет большее число разрядов (например, 271 = 256 + 8 + 4+ 2 + 1 = 2⁸ + 2³ + 2² + 2¹ + 2⁰):

у₈ у₇ у₆ у₅ у₄ у₃ у₂ у₁ у₀

1 0 0 0 0 1 1 1 1

то слева необходимо удалить лишние символы, оставив только 8 символов двоичного кода:

у₇ у₆ у₅ у₄ у₃ у₂ у₁ у₀

0 0 0 0 1 1 1 1.

Таким образом, в качестве события Y нами выбрана в соответствии с вариантом 130 кодовая комбинация 1 0 0 0 0 0 1 0.

Рассмотрим гипотезу Н₁, что была передана команда 1: 1 0 0 0 0 0 0 0, т.е. исказился второй младший разряд, вместо 0 передана 1. Вероятность справедливости этой гипотезы Р(Н₁) до появления события Y равна: Р(Н₁) = р_п1 = 0,8.

Определим условную вероятность P(Y/H₁) того, что принятая кодовая комбинация есть искаженная гипотетически переданная кодовая комбинация, соответствующая команде 1:

P(Y/H₁) = р_с⁷∙q = р_с⁷∙(1 - р_с) = 0,6⁷∙(1 – 0,6) = 0,01112.

Рассмотрим теперь гипотезу Н₂, что была передана команда 2: 1 1 1 1 1 1 1 0, т.е. исказились 5 разрядов с 3-го по 7-й включительно, когда вместо 0 передана 1. Вероятность справедливости этой гипотезы Р(Н₂) до появления события Y равна: Р(Н₂) = р_п2 = 0,2.

Определим условную вероятность P(Y/H₂) того, что принятая кодовая комбинация есть искаженная гипотетически переданная кодовая комбинация, соответствующая команде 2:

P(Y/H₂) = р_с³∙q⁵ = р_с³∙(1 - р_с)⁵ = 0,6³∙(1 – 0,6)⁵ = 0,00221.

Используя формулы Байеса, рассчитаем условные вероятности передачи команды 1 - P(H₁/Y) и команды 2 - P(H₂/Y) после появления события Y.

P(H₁/Y) = .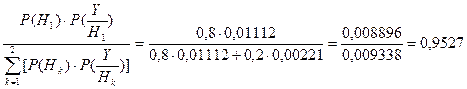

P(H₂/Y) = .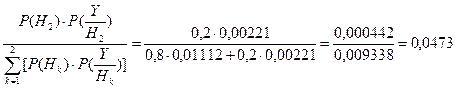

Сравнивая полученные условные вероятности двух событий, приходим к выводу, что при появлении на выходе кодовой комбинации (1 0 0 0 0 0 1 0) с вероятностью 0,9527 была передана команда 1, которой по условию соответствует кодовая комбинация (1 0 0 0 0 0 0 0).