Методические указания по выполнению задания № 3

Пусть Y – событие, состоящее в приеме кодовой комбинации 10110101, которая выбрана нами в качестве примера. Так как, какая из двух команд передана, нам неизвестна, поэтому будем рассматривать две гипотезы (предположения): Н₁ – была передана команда 1 управления и Н₂ – была передана команда 2 управления, кодовые комбинации х₈х₇х₆х₅х₄х₃х₂х₁ которых, например, равны соответственно: 11111111 и 00000000.

Допустим, что согласно условию нашей задачи, априори (т.е. до получения конкретной комбинации Y) значения вероятностей этих гипотез нам известны и равны, например: Р(Н₁) = р_п1 = 0,7; Р(Н₂) = р_п2 = 0,3. Сравнивая поразрядно значения символов y_i принятой комбинации со значениями соответствующих символов х_i гипотетически переданной комбинации, можно найти условную вероятность того, что принятая кодовая комбинация есть искаженная гипотетически переданная кодовая комбинация. Если при сравнении значений двух одноименных разрядов с индексом i имеет место равенство y_i = х_i, то, следовательно, искажение значения символа данного разряда отсутствует, а вероятность этого события согласно заданному условию равна р_с. Если же при сравнении имеет место неравенство значений y_i ≠ х_i, то это говорит об искажении значения данного символа в процессе его передачи по каналу связи под воздействием помех, а вероятность данного события равна q_с = (1 - р_с). Последовательно перемножая вероятности этих событий по результатам сравнения, получим искомое значение условной вероятности той или иной гипотезы.

Так, например, в нашем случае условная вероятность приема искаженной кодовой комбинации 10110101 вместо 11111111 равна:

Р(Y /Н₁) = р_с ∙ q_с ∙ р_с ∙ р_с ∙ q_с ∙ р_с ∙ q_с ∙ р_с = 0,6∙0,4∙0,6∙0,6∙0,4∙0,6∙0,4∙0,6 = 0,004977.

Аналогично условная вероятность приема искаженной кодовой комбинации 10110101 вместо 00000000 равна

Р(Y /Н₂) = q_с ∙ р_с ∙ q_с ∙ q_с ∙ р_с ∙ q_с ∙ р_с ∙ q_с = 0,4∙0,6∙0,4∙0,4∙0,6∙0,4∙0,6∙0,4 = 0,002212.

Решение о том, какая команда была передана, принимается на основе анализа результатов расчета условных вероятностей случайных событий по формулам Байеса с использованием значений полученных нами ранее апостериорных (т.е. после получения кодовой комбинации Y) вероятностей Р(Y /Н₁) и Р(Y /Н₂) гипотез (Н₁ и Н₂):

.

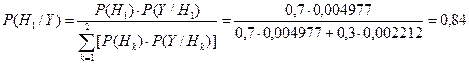
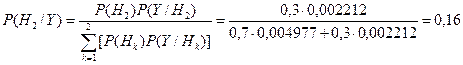Сравнивая найденные условные вероятности, приходим к заключению, что при появлении на выходе комбинации 10110101 с вероятностью 0,84 была передана команда 1, которой по условию соответствует кодовая комбинация 11111111.

Чтобы составить требуемую принятую кодовую комбинацию Y двоичного кода необходимо проставить веса всех восьми его единичных разрядов, которые представляют собой десятеричные эквиваленты единичных разрядов. Для этого необходимо взять 8-разрядную кодовую комбинацию двоичного кода, состоящую из одних единиц: 1 1 1 1 1 1 1 1 и проставлять веса единичных разрядов, которые равны 2^n-1, начиная с первого левого (младшего) разряда и кончая восьмым правым (старшим) разрядом, где – n – есть текущий номер разряда:

2⁷ 2⁶ 2⁵ 2⁴ 2³ 2² 2¹ 2⁰ = 128 64 32 16 8 4 2 1.

Десятеричный эквивалент двоичного числа равен сумме весов всех его единичных разрядов, т.е. 11111111₂ = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255₁₀.

По условию задачи ваши три последние цифры шифра представляют собой десятеричный эквивалент вашей кодовой комбинации. Вам остается только набрать в сумме из весов единичных разрядов (веса не должны повторяться) ваше трехразрядное число. Те номера разрядов, веса которых вы использовали, должны иметь в вашей кодовой комбинации единичные значения, а остальные разряды иметь нулевые значения.

Примеры. 1. Допустим, три последних цифры вашего шифра имеют нулевые значения, 000₁₀. При отсутствии значащих цифр все разряды имеют нулевые значения: 000₁₀ = 00000000₂.

2. 001₁₀ = 1 (вес у₁) = 00000001₂

3. 011₁₀ = 8 (вес у₄) + 2 (вес у₂) + 1 (вес у₁) = 00001011₂.

4. 111₁₀ = 64 (вес у₇) + 32 (вес у₆) + 8 (вес у₄) + 4 (вес у₃) + 2 (вес у₂) + 1 (вес у₁) = 01101111₂.

Примечание. Индексы 10 и 2 указывают на основание системы счисления, в которой представлено число, соответственно, в десятичной или двоичной системах счисления.