Д) Параллель жалғанған қоректендіргіштерді бір балама қоректендіргішпен айырбастауға (түрлендіруге) болады (5-сурет) .

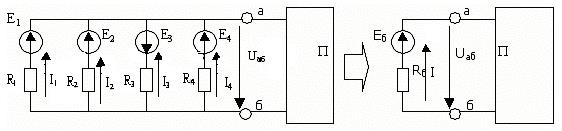
5-сурет

Кирхгофтың бірінші заңы бойынша: I=I₁+I₂+I₃+I₄, немесе

(E_б – U_аб)/R_б =(E₁ – U_аб)/R₁+(E₂ – U_аб)/R₂ +(-E₃ – U_аб)/R₃+(E₄ – U_аб)/R₄. Бұдан

E_б= (E₁G₁+ E₂G₂-E₃G₃+E₄G₄ )/(G₁+G₂+G₃+G₄ ), 1/R_б=1/R₁+1/ R₂+1/ R₃+1/R₄= G₁+G₂+G₃+G₄.

Жалпы жағдайда У_б= /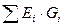

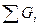
Электр тізбегінің негізгі принциптері (қасиеттері). 1)Беттестіру принципі: Егер тізбекте бірнеше электр қозғаушы күштер болса, онда осы тізбектің кез келген тармағындағы ток осы электр қозғаушы күштердің сол тармақта әрқайсы тудырған токтарының алгебралық қосындысына тең.

2)Теңгеру принципі: Тізбектің тармағындағы кедергіні сандық мәні сол кедергі мен токтың көбейтіндісіне тең, ал бағыты токтың бағытына қарама- қарсы электр қозғаушы күшімен айырбастауға болады.

3)Өзаралық принцип: Тізбектің k тармағына орналасқан э.қ.к. m тармағында I_m (I_m=E_к ∙G_km) тогын тудырса, онда m тармағындағы э.қ.к. Е_m=E_к k тармағында мәні I_m-ге тең I_k (I_к =E_m ∙G_mk )тогын тудырады. G_km , G_mk -өзаралық өткізгіштіктер.

Қуаттар балансы:Тізбектегі қоректендіргіштердің қуаттарының алгебралық қосындысы сол тізбектегі тұтынушылардың қуаттарының арифметикалық қосындысына тең. Қоректендіргіштің қуаты

Р_қ =E∙I, ал тұтынушы қуаты P_т =I² ∙R формулалары арқылы анықталады.

Потенциалдық диаграмма потенциалдың тізбектің өн бойындағы өзгерісін сипаттайды. Тізбектің бір нүктесінің потенциалын нөлге тең деп алады да, қалған нүктелердің потенциалдарын осы нүктенің потенциалымен салыстыра отырып анықтайды. Абцисса осіне масштаб бойынша кедергілерді салады, ал ордината осінде потенциалдарды көрсетеді.

Негізгі әдебиеттер: [1(21-24, 33-35, 42-54), 3(71-74, 80-91, 94-96, 104-108)]

Қосымша әдебиеттер: [ 4,5,7,8]

Бақылау сұрақтары:

1.Бір э.қ.к-і бар электр тізбектерін есептеу. Балама түрлендіру тәсілі. Кедергілердің бірізді, параллель және аралас жалғануы.

2.Кедергілердің жұлдызша және үшбұрыштап жалғануы.

3.Э.қ.к-тердің бірізді және параллель жалғануы. Балама генератордың параметрлері.

4.Электр тізбегінің негізгі принциптері

5.Қуаттар тепе-теңдігі. Потенциалдық диаграмманы құру.

Дәріс. Тұрақты токтың бірнеше э.қ.к.-тері бар күрделі тізбектерін есептеу тәсілдері. Кирхгоф заңдарын пайдалану арқылы есептеу тәсілі. Контурлық токтар тәсілі. Түйіндік потенциалдар тәсілі

Тұрақты токтың күрделі тізбектерін есептеу үшін мынандай тәсілдерді қолдануға болады:

1) Кирхгофтың заңдарын пайдаланып есептеу тәсілі; 2) Контурлық токтар тәсілі; 3) Түйіндік потенциалдар тәсілі; 4) Екі түйіндік тәсіл; 5) Балама генератор тәсілі.

Кирхофтың заңдарын пайдалану арқылы есептеу тізбектің тармақтарындағы анықталуға тиісті токтарға қатысты теңдеулер құрудан басталады. Құрылатын теңдеулер саны белгісіз токтар санына тең. Кирхгофтың бірінші заңы бойынша құрылатын теңдеулер саны тізбектегі түйін санынан біреуге кем болады, яғни т-1 тең.Мұндағы т- тізбектегі түйіндер саны. Кирхгофтың екінші заңы бойынша құрылатын теңдеулер саны жалпы құрылатын теңдеулер саны мен бірінші заңы бойынша құрылатын теңдеулер санының айырмасына тең, яғни к -( т-1). Мұндағы к-тізбектегі тармақтар саны. Кирхгофтың екінші заңы бойынша теңдеулер құру кезінде басқа контурға кірмеген тармағы бар тәуелсіз контурлар үшін құруға тырысқан жөн.

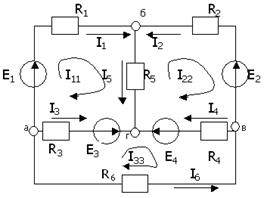
Кирхгофтың заңдары бойынша

6-суретте көрсетілген тізбек үшін теңдеулер құру:

Түйіндер үшін

а) –I₁– I₆ – I₃ =0

б) I₁+I₂ – I₅ =0

в) I₆ – I₂ – I₄ =0

Контурлар үшін

1-контур) E₁ – E₃=I₁∙R₁+I₅∙R₅ – I₃∙R₃

2-контур) –E₂+E₄= -I₂∙R₂+I₄∙R₄ – I₅∙R₅

3-контур) E₃ – E₄= –I₆∙R₆–I₄∙R₄ + I₃∙R₃

Теңдеулер жүйесін өзімізге белгілі әдестер арқылы шешеміз де, I₁,I₂,I₃,I₄,I₅,I₆ токтарды табамыз

6-сурет

2.Контурлық токтар тәсілі. Бұл тәсілді қолданған кезде электр сұлбасының тәуелсіз контурында тек өзінің контурлық тогы жүреді деп есептейді. Контурлық токдеп қарастырылған контурдың барлық тармақтарымен жүреді деп шартты түрде қабылданған ток. Бұл тәсіл бойынша теңдеулер Кирхгофтың екінші заңы бойынша контурлық токтарға байланысты құрылады. Сондықтан есептеу жұмысы көп жеңілдейді.

Контурлық токтар тәсілінің есептеу жұмысында қолданылуын 6-суретте көрсетілген тізбектің тармақтарындағы токтарды анықтау арқылы қарастырайық. Әрбір контур үшін контурлық токтың бағытын өз қалауымызша, мысалы сағат тілінің жүрісінің бағытымен бағыттас етіп таңдап аламыз. Екі контурға ортақ тармақпен жүретін контурлық токтар бағыттас болса, онда олардың қосындысы алынады. Керісінше жағдайда олардың айырмасын алады. Жалпы жағдайда қарастыралатын тізбек үшін теңдеулер мынадай түрде жазылады:

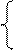Е₁₁= I₁₁∙R₁₁+ I₂₂∙R ₁₂ + I ₃₃∙ R ₁₃

Е₂₂= I₁₁∙R₂₁+ I₂₂∙R ₂₂ + I ₃₃∙ R ₂₃

Е₃₃= I₁₁∙R₃₁+ I₂₂∙R ₃₂ + I ₃₃∙ R ₃₃

Мұндағы Е₁₁, Е₂₂, Е₃₃- бірінші, екінші және үшінші контурлардың контурлық э.қ.к.-тері;

R₁₁, R₂₂, R ₃₃- бірінші, екінші және үшінші контурлардың өзіндік кедергілері,

R₁₁= R₁+R₅ +R₃; R₂₂= R₂+R₄+R₅; R ₃₃= R₆+R₄ +R₃.

R ₁₂=R₂₁- бірінші мен екінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

R₁₃= R₃₁- бірінші мен үшінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

R ₂₃= R ₃₂- екінші мен үшінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

Теңдеулер 6-суретте көрсетілген тізбек үшін былай жазылады:

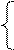E₁ – E₃=I₁₁∙(R₁+R₅ +R₃) – I₂₂∙R₅ –I₃₃∙R₃

– E₂+E₄= I₂₂∙ (R₂+R₄+R₅) – I₃₃∙R₄ –I₁₁∙R₅

E₃ – E₄=I₃₃∙ (R₆+R₄ +R₃) – I₁₁∙R₃– I₂₂∙R₄

Әр теңдеудегі жақшаның ішінде кедергілердің қосындысы контурдың өзіндік кедергісі деп аталады. Теңдеулер жүйесін шешеміз де I_11, I_22, I₃₃ контурлық токтарын табамыз. Тармақтардың токтарын (I₁ ... I₆) контурлық токтар арқылы табамыз:I₁=I₁₁, I₂= –I ₂₂, I₃= I₃₃ – I₁₁, I₄=I₂₂–I₃₃, I₅=I₁₁ – I₂₂, I₆= –I₃₃

3.Түйіндік потенциалдар тәсілі.Сұлбалардағы түйіндердің потенциалдарын белгісіз ретінде қабылдап, электр тізбектерін есептеу тәсілін түйіндік потенциалдар тәсілі деп атайды.Айталық, сұлбада n-түйін болсын. Сұлбаның кез-келген бір нүктесін ойша жермен қосамыз, яғни оның потенциалын нөлге тең деп аламыз.Соның нәтижесінде белгісіздер саны n-1-ге дейін азаяды. Бұл тәсіл бойынша теңдеулер Кирхгофтың бірінші заңы бойынша түйінде түйіскен токтарға арнап құрылады. Токтарды түйіндердің потенциалдары арқылы Ом заңы бойынша өрнектеуге болады. Нәтижесінде теңдеулер жүйесі мынадай түрде жазылады:

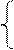φ₁G₁₁ + φ₂G₁₂ + φ₃G₁₃= I₁₁

φ₁G₂₁ + φ₂G₂₂ + φ₃G₂₃= I₂₂

φ₁G₃₁ + φ₂G₃₂ + φ₃G₃₃= I₃₃

φ₁, φ₂, φ₃- бірінші, екінші және үшінші түйіндердің потенциалдары; G₁₁, G₂₂, G₃₃-- бірінші, екінші және үшінші түйіндерде түйіскен тармақтардың өткізгіштердің қосындысы; G_km- k мен m түйіндерді байланыстыратын тармақтың өткізгіштігі, “минус” таңбасымен алынады; I₁₁, I₂₂, I₃₃- түйіндердің түйіндік токтары. Белгілі бір түйіннің түйіндік тогы сол түйінмен байланысқан тармақтардағы э.қ.к.-терді сол тармақтардың кедергілеріне бөлу арқылы табылған токтардың алгебралық қосындысына тең. Э.қ.к.-тері түйінге бағытталған тармақтардың токтары «плюс» таңбасымен алынады, ал керісінше жағдайда «минус»таңбасы алынады.

Берілген тізбектің (6-сурет) « г» түйінінің потенциалын нөлге тең деп аламыз.Теңдеулер көрсетілген тізбек үшін былай жазылады:

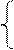φ_а(g₁+g₃+g₆) - φ_бg₁ - φ_вg₆= -E₁g₁-Е₃g₃

φ_б(g₁+g₂+g₅) - φ_аg₁ - φ_вg₂= E₁g₁ + E₂g₂

φ_в(g₂+g₄+g₆) - φ_бg₂ - φ_аg₆= -E₂g₂ -E₄g₄

Мұндағы g₁=1/R ₁, g₂=1/R₂, g₃=1/R₃ , g₄=1/R₄ , g₅=1/R₅ , g₆=1/R₆.

Теңдеулер жүйесін шешу арқылы φ_а, φ_б, φ_в табамыз. Токтардың мәндерін Ом заңы арқылы табамыз:

I₁= (E₁+ U_аб)/R₁ = [E₁+(φ_а - φ_б)]/R₁, I₂= (E₂+ U_вб)/R₂=[E₂+(φ_в- φ_б) ]/R₂, I₃= (E₃+ U_аг)/R₃=[E₃+ (φ_а - φ_г) ]/R₂

I₄= U_вг/R₄=(φ_в - φ_г)/R₄ = φ_в/R₄ I₅= U_бг/R₅=(φ_б - φ_г)/R₄ = φ_б/R₅ I₆= (E₆+ U_ав)/R₆=[ E₆+ (φ_а - φ_в) ]/R₆

Негізгі әдебиеттер: [1(24-33, 35-40), 3(68-71, 74-80, 98-103)]

Қосымша әдебиеттер: [ 4,5,7,8]

Бақылау сұрақтары:

1.Бірнеше э.қ.к-ілері бар күрделі тұрақты ток тізбектерін есептеу тәсілдері. Ом және Кирхгоф заңдарын пайдалану арқылы есептеу.

2.Контурлық токтар тәсілі.

3.Түйіндік потенциалдар тәсілі.

№4 Дәріс. Екі түйіндік тәсіл. Екіұштықтар. Балама генератор тәсілі. Энергияны активті екіұштықтан пассивті екіұштыққа беру

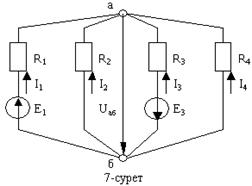Екі түйіндік тәсіл. Көп жағдайда екі түйіннен тұратын электр сұлбалар кездеседі. Мұндай сұлбаларды есептеу үшін түйіндік потенциалдар тәсілінің жеке бір түрі –екі түйіндік тәсілді қолданған тиімді. Бұл тәсіл бойынша екі түйін арасындағы кернеуді табу арқылы тармақтардағы токтарды анықтайды. Мысалы, 7-суреттегі тізбектің тармақтарындағы токтарды табайық. Ол үшін алдымен U_аб кернеуін табамыз. Тізбектің «б » түйінінің потенциалын нөлге тең деп аламыз. Сонда U_аб=φ_а – φ_б = φ_а – 0 = φ_а.

Тізбектің «а » түйіні үшін: I₁ + I₂ +I₃ + I₄=0,

мұндағы I₁= (E₁ - U_аб)/R₁=(E₁-φ_а)/R₁,

I₂= - U_аб . R₂= -φ_а . R₂, I₃= (-E₃ - U_аб).R ₃=(-E₃-φ_а).R₃, I₄= -φ_а . R₄.

Токтардың өрнектерін теңдеуге қоямыз да , φ_а табамыз:

φ_а(g₁+g₂+g₃+g₄)= E₁g₁ – E₃g₃,

φ_а=(E₁g₁ – E₃g₆)/ (g₁+g₂+g₃+g₄).

Табылған φ_а мәнін токтардың өрнектеріне қойып, олардың мәндерін анықтаймыз. Табылған φ_а мәнін токтардың өрнектеріне қойып, олардың мәндерін анықтаймыз. Жалпы жағдайда U_аб =∑ E_кg_к /∑g_к.

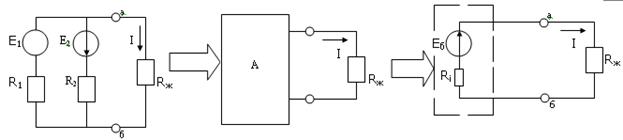
Балама генератор тәсілі.Бұл тәсіл күрделі тізбектің бір тармағындағы токты табу үшін қолданылады. Бұл тәсіл бойынша есептеу үшін қарастырылатын тармақты тізбектің басқа бөлігінен бөліктеп аламыз. Қалған бөлікті активті екіұштық деп қарастырамыз. Активті екіұштық дегеніміз екі ғана жалғану ұшы бар, ал ішінде э.қ.к. мен резисторлар бар тізбекті айтамыз (8-сурет).

8-сурет

Егер екіұштықтың ішінде энергия көзі (қоректендіргіш) болмаса, онда оны пассивты екіұштық дейді және оны электр энергиясын қабылдаушы деп санайды. Балама сұлбада пассивты екіұштықты бір кедергімен бейнелейді. Ол кедергіні екіұштықтың ішкі немесе кірістік кедергісі деп атайды.

Тізбектің бөлектенген тармағына байланысты активті екіұштықтықты балама генератормен айырбастауға болады. Бұл генератордың э.қ.к.-і E_б бос жүріс режимі кезінде бөлектенген тармақтың қысқыштарындағы кернеуге U_бж тең, ал _, ішкі кедергісі R_б екіұштықтықтың кірістік кедергісі R_i тең.

Қарастырылатын тармақтағы токты табуды мынадай ретпен жүргізген жөн:

а)E_б-ні табу үшін бос жүріс режимін қарастырамыз, яғни тогы анықталуға тиісті тармақты а және б нүктелерінде үзіп, екіұштыдан оны айырып тастаймыз. Онан кейін а және б нүктелерінің арасындағы кернеуді U_аббж есептік жолмен немесе өлшеу арқылы табамыз.

ә) Генератордың ішкі кедергісі R_б табу үшін а және б нүктелеріне байланысты екіұштықтың толық кедергісін анықтаймыз. Ол үшін екіұштықтың сұлбасындағы э.қ.к.-терді алып тастап, олардың орындарын қысқы тұйықтаймыз. Сұлбада тек кедергілерді қалдырамыз.

б) Қарастырылатын тармақтағы токты мына формула бойынша табамыз: I= U_аббж /( R_ж+ R_i) .

Егер қарастырылатын тармақтың кедергісін нөлге теңестірсе ( R_ж =0), онда ол үшін қысқаша тұйықталу режимі орын алады. Тармақпен қысқаша тұйықталу тогы (I_қ.т) жүреді: I_қ.т= U_аббж /R_і. Бұдан

R_і .=U_аббж /I_қ.т , яғни ішкі кедергіні табу үшін бос жүріс режимі кезінде өлшенген кернеуді U_аббж қысқаша тұйықталу режимі кезінде өлшенген токқа I_қ.т бөлу керек.

Энергияны активтік екіұштықтан жүктемеге беру. Активті екіұштыққа қосылған жүктемеде R_ж бөлінетін қуат P = I² R = U_аббж R_ж /( R_ж+ R_i). Қабылдағышқа максимал қуат беру шартын анықтау үшін P-ның R_ж бойынша бірінші ретті туындысын тауып,оны нөлге теңейміз. Осыдан R_ж = R_i. Демек осы теңдік орындалған жағдайда жүктемеде максимал қуат бөлінеді: P_max= U²_аббж /4R_і. Балама генераторда бөлінетін толық қуат P_тол =U_аббж I =U²_аббж /( R_ж+ R_i). Пайдалы әсер коэффициенті ( п.ә.к.): η= P/ P_тол = R_ж /( R_ж+ R_i). Егер R_ж = R_i болса, онда η=0,5.

Активті екіұштықтың кірістік кедергісіне R_i тең жұктеме кедергіні R_ж келістіру немесе үйлестіру жүктемесі деп атайды.

Байланыс жүйелерінде, электроникада көп жағдайда қабылдағышқа максимал қуат берудің маңызы зор.

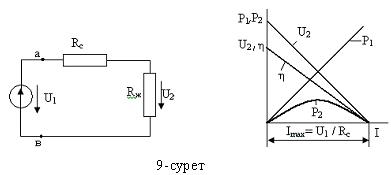
Беріліс желісі арқылы энергияны тасымалдау.Электр желісінің сұлбасы 9а-суретте бейнеленген, мұндағы U₁ –желінің басындағы генератордың кернеуі; U₂ – желінің соңындағы жүктеменің кернеуі; R_с –желінің сымдарының кедергісі; R_ж – жүктеменің кедергісі.

Нақты желілер арқылы үлкен қуат бергенде η = 0,94...0,99 болса онда U₂ кернеуі U₁ – ден бірнеше пайызға кіші болады. Өте үлкен қуатты алыс қашықтыққа тасымалдағанда п.ә.к.- тің жоғары болуы экономикалық жағынан тиімді. Желінің басындағы қуаттың P₁ және жүктемедегі қуаттың P₂ , п.ә.к пен U₂ –нің жүктемедегі токта тәуелді өзгерістерін сипаттайтын сызықтар 9ә-суретте бейнеленген. Олар төмендегі теңдеулер негізінде салынған: P₁=U₁I; P₂=U₁I- I² R_с; η = R_ж /( R_ж+ R_с); U₂=U₁ - I R_с. Токтың максималдық мәні I_max = U₁ / R_с жүктеменің қысқаша тұйықталу кезінде орын алады.

Желінің п.ә.к.-інің мәні U₁ кернеуі неғұрлым жоғары болған сайын, соғұрлым жоғары болады.

Негізгі әдебиеттер: [1(40-41, 54-58), 3(97-98, 109-118)]

Қосымша әдебиеттер: [ 4,5,7,8]

Бақылау сұрақтары:

1.Қандай тізбектерді есептеу үшін екі түйіндік тәсіл қолданылады? Бұл тәсіл бойынша тізбекті есептеу қалай жүргізіледі?

2.Қандай жағдайда тізбекті есептеу үшін балама генератор тәсілін қолданады? Бұл тәсіл бойынша тізбекті 9-сурет есептеу қалай жүргізіледі?

3.Энергияны активті екіұштыдан пассивті екі ұштыға беру. Қабылдағышқа максимал қуат беру шарты қандай? Пайдалы әсер коэффициенті ( п.ә.к.) қалай анықталады?

4.Энергияны беріліс желісі арқылы тасымалдаған кезде жүктемедегі кернеудің, жүктемеде бөлінетін қуаттың және п.ә.к.-тің токқа тәуелді өзгерістерінің сипаты қандай?