Пересечения прямой с поверхностью многогранника

Поверхность многогранника представляет собой совокупность пересекающихся плоскостей. Поэтому решение данной задачи, по существу, является двукратным определением точки пересечения прямой линии с плоскостью (см. раздел 3.2, рис.35).

Схема решения выглядит так:

- плоскость S, проходящая через прямую n, пересечет многогранник по плоской замкнутой ломаной линии 1-2-3-1;

- искомые точки M и N есть результат пересечения линии 1-2-3-1 с прямой n.

Алгоритм решения задачи:

1. S É n, S -проецирующая плоскость.

2. S Ç F = ( 1-2-3-1).

3. М =(1-2-3-1) Ç n = F Ç n,

N = ( 1-2-3-1) Ç n = F Ç n.

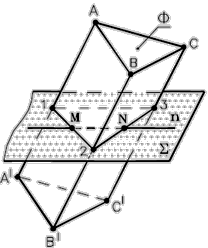
Рисунок 3 – Определение точек пересечения прямой с поверхностью многогранника (пространственный пример)

ПРИМЕР: Определить точки М и N пересечения прямой общего положения n с поверхностью Фпирамиды SABC.

Построение:

1. Через прямую nпроводим горизонтально проецирующую плоскость S.

2. Определяем горизонтальную проекцию ломаной: S₁ Ç Ф₁ = (1₁ – 2₁ – 3₁- 1₁).

3. Определяем фронтальные проекции вершин ломаной: 1₂ Ì А₂ В₂, 2₂ Ì S₂B₂, 3₂ Ì B₂C₂.

4. Строим фронтальную проекцию ломаной: 1₂ – 2₂ – 3₂- 1₂.

5. Определяем фронтальные проекции искомых точек: (1₂ – 2₂ – 3₂- 1₂) Ç n₂ = М₂ Ù N₂.

6. Определяем горизонтальные проекции точек: М₁ Ì n₁ Ù N₁ Ì n₁.

7. Определяем видимость проекций прямой nпо видимости проекций граней пирамиды.

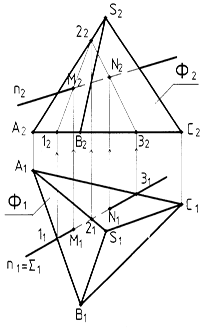
Рисунок 4 – Определение точек пересечения прямой с поверхностью пирамиды

Контрольные вопросы:

1. Что называется многогранником?

2. Условие принадлежности точки многограннику?

3. Из каких элементов состоит гранная поверхность?

4. Какое сечение называют нормальным?

5. Как образуется призматическая поверхность?

6. Как образуется поверхность пирамиды?

7. Назовите призматические сечения.

8. Назовите конические сечения пирамиды.

9. В чем заключается способ нахождения точек пересечения многогранной поверхности с прямой линией?

10. Как определить видимость проекций прямой пересечения с многогранником?