Сечение многогранников плоскостью

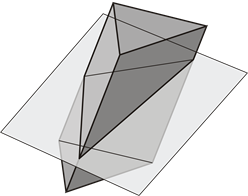
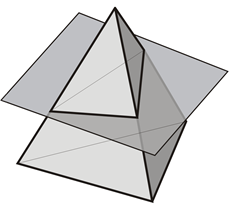
При пересечении многогранника плоскостью получается плоский много­угольник. Вершинами этого многоугольника являются точки пересечения ребер с секущей плоскостью, а сторонами - линии пересечения граней с секущей плоскостью.

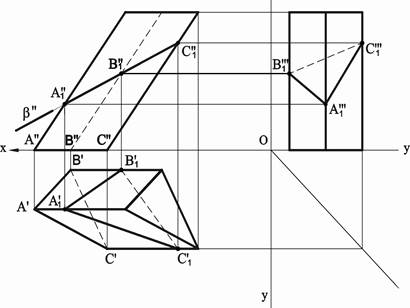
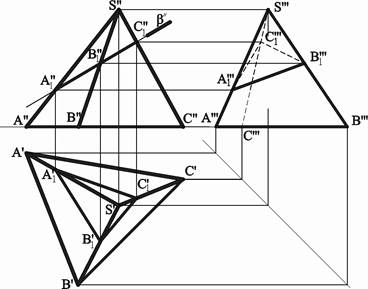
Построение сечений многогранников плоскостью сводится, во-первых, к нахождению точек пересечения ребер многогранника с секущей плоскостью и, во-вторых, последовательному соединению построенных точек с учетом видимости граней многогранника (рисунок 2). Последовательное соединение предполагает соединение пары точек, принадлежащих одной грани многогранника. Так, в обоих примерах, приведенных ниже, фронтально-проецирующие плоскости β пересекают наклонную трехгранную призму и трехгранную пирамиду по треугольникам A1B1C1, где точки A1, B1, C1 есть точки пересечения плоскостей β с боковыми ребрами призмы и пирамиды.

Рисунок 2

При построении проекций нормального сечения призмы необходимо помнить о том, что секущая плоскость должна быть перпендикулярна боковым ребрам призмы.