Точки на поверхностях многогранников

Так как поверхность многогранника есть плоскость, для нахождения точки необходимо провести вспомогательную линию в грани многогранника с учётом взаимности.

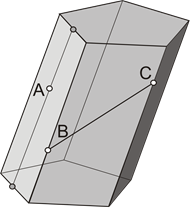
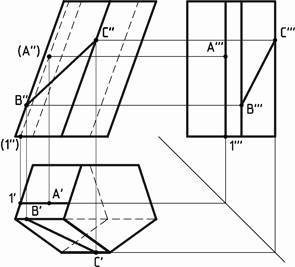
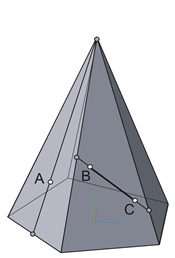
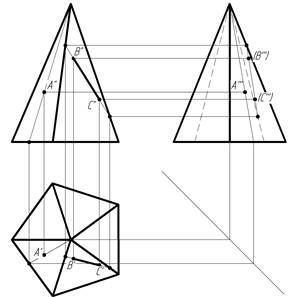
Построение точек и линий на гранях многогранников аналогично построению точек и линий в плоскости. В качестве примера на рисунке 1 дано наглядное изображение призмы и пирамиды, на гранях которых построены прямые и точки: прямые BC имеют с гранями две общие точки (на ребрах), а точки A находятся на прямых, принадлежащих этим граням. На трехпроекционном чертеже показано построение точки A, принадлежащей боковой грани пирамиды и наклонной призмы, и отрезка BC, принадлежащего также боковым граням. Точка A построена с помощью вспомогательной прямой, принадлежащей грани призмы и пирамиды.

Рисунок 1