Завдання № 5/2. Розрахунок молекулярної суми за станами Q

2.1. Довести, що молекулярну суму за станами Q для ідеального газу може бути подано у вигляді добутку

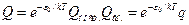, (8)

де Q_пост. - сума за станами поступального руху; Q_вн. - сума за внутрішньомолекулярними станами; ε₀ - енергія молекули на нульовому енергетичному рівні.

2.2. Показати, що величину Q_вн. у формулі (8) у свою чергу може бути представлено як добуток обертальної (Q_об.), коливальної (Q_кол.) і електронної (Q_ел.) складових:

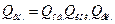. (9)

2.3. З урахуванням (8) показати, що при виділенні нульової енергії формули (3) - (7) для 1 моля ідеального газу мають вигляд:

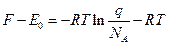; (10)

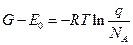; (11)

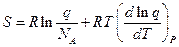; (12)

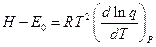; (13)

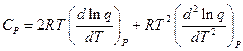; (14)

2.4. Вивести формули для поступальної, обертальної та коливальної складових молекулярної суми за станами. Показати, що вони можуть мати вигляд:

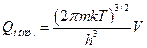; (15)

для лінійних молекул:

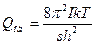; (16)

для нелінійних молекул:

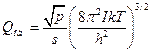; (17)

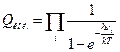, (18)

де m - маса частинки; V - об'єм газу; І - момент інерції молекули; s- число симетрії; ν_i - частота і-го виду коливань.

2.5. Обчислити поступальні, коливальні та повні молекулярні суми за станами для певного ідеального газу. Об'єкт та температура для розрахунку задаються викладачем.