ПРАКТИЧЕСКОЕ ЗАЕЯТИЕ § 3. Метод Фурье

10. Метод Фурье. Мы рассмотрим в этом параграфе за­дачу о свободных колебаниях струны, закрепленной на обоих концах. Как указано в § 1, задача сводится к решению одно­родного уравнения струны

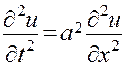(3,1)

при начальных условиях

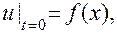
(3,2)

и краевых условиях

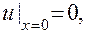
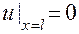(3.3)

Метод Фурье (или, как его еще называют, метод раз­деления переменных) принадлежит к -числу важнейших ме­тодов решения уравнений математической физики. Мы с ним будем в дальнейшем неоднократно встречаться.

Первая часть метода Фурье состоит в том, что мы отыскиваем частные решения уравнения (3.1), удовлетворяющие краевым условиям (3.3), вида

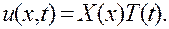(3.4)

Каждое из искомых частных решений, таким образом, представляется в виде произведения двух функций, одна из которых зависит только от х, а другая — только от t.

Дифференцируя дважды выражение (3.4) по х и по t, получим

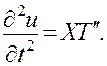
(Для сокращения записи мы не пишем аргументов функций Х(х) и T(t).)

Подставляя выражения для производных в уравнение (3.1), получим

или, деля обе части равенства на произведение ,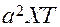

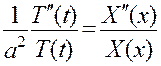(3.5)

Чтобы функция 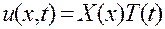была решением уравнения (3.1), равенство (3.5) должно соблюдаться при всех зна­чениях х и t. Левая часть этого равенства зависит только от переменной t и не может изменяться при изменении х. Поэтому, если зафиксировать t и менять х, левая часть, а следовательно и правая, будет сохранять постоянное зна­чение. Рассуждая аналогично, установим, что правая часть, а следовательно и левая, не может изменяться и при изме­нении t. Это будет справедливо только в том случае, когда обе части равенства (3.5) вообще не зависят ни от х, ни от t, т.е. 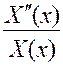когда оба отношения и являются величинами постоянными:

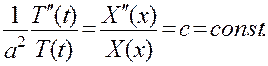(3.6)

Отсюда следует, что функции T и X должны удовле­творять дифференциальным уравнениям

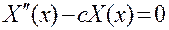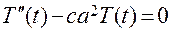и (3.7)

Поскольку мы ищем частные решения, удовлетворяющие краевым условиям (3.3), то при любом значении t должны соблюдаться равенства

.

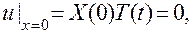
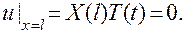Если бы обращался в нуль второй множитель, то реше­ние 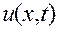равнялось бы пулю при всех значениях х и t. Поэтому, чтобы отыскать решения, не тождественно равные нулю (а только такие нас и интересуют), мы должны счи­тать, что

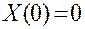и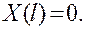

В результате для отыскания функции Х(х) мы пришли к следующей задаче { Эта задача является частным случаем общей задачи Штурма—Лиувилля, заключающейся в отыскании решений линей­ного дифференциального уравнения второго порядка вида , удовлетворяющих некоторым краевым усло­виям, т. е. условиям, налагаемым на искомую функцию или ее про­изводную в точках х = а и х=b (концах интервала).}: найти решения линейного дифферен­циального уравнения второго порядка

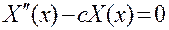(3.8)

при условиях

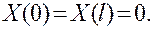(3.9)

Разумеется, эта задача при любом с имеет решение, то­ждественно равное нулю: 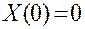. Оказывается, однако, что при некоторых значениях постоянной с эта задача имеет и другие решения.

Заметим, что в этом состоит существенное отличие реше­ния рассматриваемой задачи от решения обыкновенных диф­ференциальных уравнений с начальными условиями, когда для определения частного решения задаются значения функции и ее производной в некоторой начальной точке. Как известно (см. введение), последняя задача имеет единственное решение.

Полагая 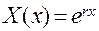, составим для уравнения (3.8) харак­теристическое уравнение

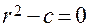
и рассмотрим различные случаи.

1. Пусть 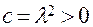. Тогда корни характеристического уравнения действительны, 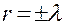, и общее решение урав­нения имеет вид

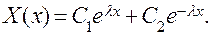
Чтобы соблюдались условия (3.9), мы должны положить

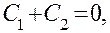
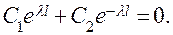
Так как определитель этой однородной системы 1 1

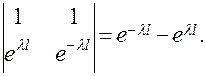
не равен нулю, то система имеет единственное решение

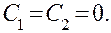
Таким образом, в этом случае решений, отличных от тожде­ственного нуля, не существует.

2. Пусть с = 0. Тогда оба корня характеристического уравнения равны нулю и

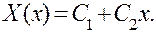
Подставляя в условия (3.9), получим

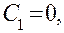
т. е. опять-таки .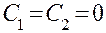

3. Пусть, наконец, 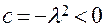. Корни характеристиче­ского уравнения чисто мнимые, 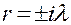, и решение будет содержать тригонометрические функции

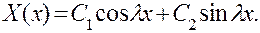
При х = 0 должно быть

,

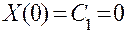а при х=l

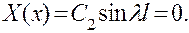
Последнее равенство возможно, когда 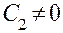, именно оно будет удовлетворяться при

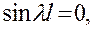
т. е. при

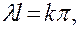
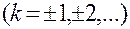
(k не равно нулю, так как по условию ).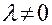

Итак, если 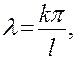т. е. то сущест­вуют решения уравнения (3.8), не равные тождественно нулю.

Решение, отвечающее некоторому фиксированному к, обозначим через 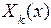. Оно имеет вид

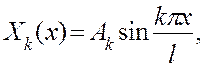(3.10)

где 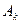— произвольная постоянная. Мы вправе в дальнейшем придавать k только положительные значения: k =1, 2,… поскольку при отрицательных k будут получаться решения того же вида (ведь 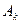— произвольные постоянные, которые могут иметь любые знаки).

Как мы видим, каждому значению 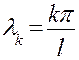соответствует бесчисленное множество решений (3.10), отличающихся друг от друга постоянным множителем.

Величины 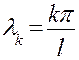называют собственными числами, а функции 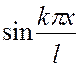собственными функциями дифферен­циального уравнения (3.8) с краевыми условиями (3.9).

Напомним читателю, что система функций 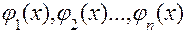называется ортогональной в интервале [а,b], если интеграл от произведения любых двух различных функций системы равен нулю: 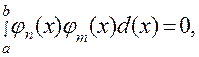если 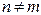(см. [1], п. 205). Легко установить, что найденные собствен­ные функции ортогональны на интервале [0, l]. Действи­тельно, при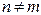

Теперь обратимся к отысканию функций T(t). Каждому собственному числу 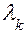будет соответствовать своя функ­ция 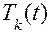, определяемая вторым из уравнений (3.7) (напоми­наем, ):

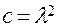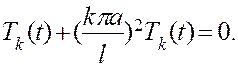
Его общее решение имеет вид

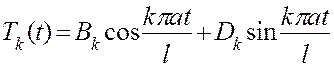(3.11)

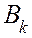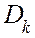где и — произвольные постоянные.

Подставляя выражения (3.10) и (3.11) в формулу (3.4), найдем частные решения уравнения (3.1), удовлетворяющие краевым условиям (3.3). При этом каждому значению k=1, 2, ... будет отвечать решение

.

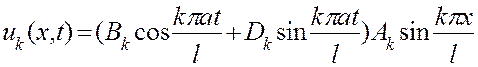Внося множитель 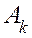в скобку и вводя обозначения 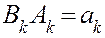и , запишем 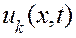в виде

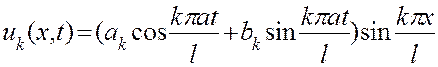. (3.12)

Решения 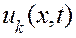называются собственными функциями задачи; соответствующие им колебания струны называются собственными колебаниями.

Физический смысл решений (3.12) мы рассмотрим не­сколько позже, а сейчас перейдем ко второй части метода Фурье и при помощи собственных функций построим реше­ние, удовлетворяющее начальным условиям (3.2). Для этого возьмем сумму решений (3.12), которая в силу линейности и однородности уравнения (3.1) также будет являться его решением:

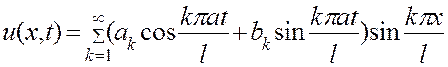, (3.13)

Поскольку мы составили бесконечный ряд, то, разумеется, нужно, чтобы он был сходящимся. Мы предположим также, что его можно дважды почленно дифференцировать (см. введение). Ясно, что функция 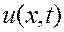удовлетворяет краевым условиям (3.3), так как им удовлетворяет каждая из функций .

Будем теперь подбирать произвольные постоянные 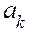и 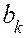так, чтобы функция (3.13) удовлетворяла начальным условиям. Подставляя значение t=0, получим

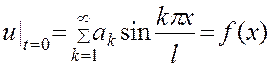. (3.14)

Дифференцируя ряд (3.13) по t;

,

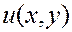и подставляя t=0, удовлетворим второму начальному усло­вию:

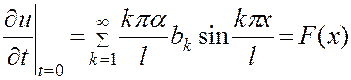(3.15)

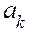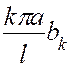Формулы (3.14) и (3.15) показывают, что величины и являются коэффициентами разложения функций f(х) и F(x) в ряд Фурье по синусам в интервале 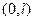(см. [1],п. 201). Вспоминая формулы для коэффициентов этого разложения, найдем :

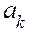(3.16)

Так как 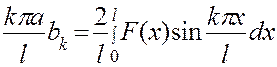, то

.

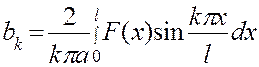Подставляя выражения для коэффициентов 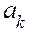и 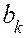в ряд (3.13), мы окончательно найдем решение поставленной за­дачи.

Мы не останавливаемся на условиях, которые надо наложить на функции f(x) и F(x), чтобы было оправдано сделан­ное допущение о возможности почленного дифференцирования ряда (3.13). Обычно в физических задачах эти условия соблю­даются.

Формула (3.13) показывает, что в моменты времени 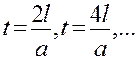струна возвращается в свое первона­чальное состояние; это означает, что колебания струны незатухающие и периодически повторяющиеся, с периодом 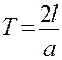. Так происходит потому, что мы пренебрегли си­лами трения. При учете их получились бы затухающие коле­бания, аналогично тому как это имеет место в случае обык­новенных гармонических колебаний точки. Решение задачи в этом случае приведено в п. 14.

ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ

ВВЕДЕНИЕ

1. Дифференциальные уравнения с частными производными. В дальнейшем будем предполагать, что читатель уже знаком с основами теории обыкновенных дифферен­циальных уравнений, т. е. уравнений, связывающих неизвест­ную функцию одной независимой переменной, ее производные и саму независимую переменную. Мы приведем лишь самые основные сведения.

Дифференциальное уравнение первого порядка вида 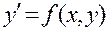имеет бесчисленное множество решений, опреде­ляемых формулой, содержащей одну произвольную посто­янную: . Аналогично общее решение дифферен­циального уравнения второго порядка 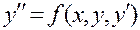со­держит две произвольные постоянные: 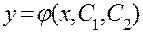. Выде­ление частного решения может быть произведено путем задания начальных условий, которые для уравнения второго по­рядка обычно имеютвид 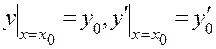. Подстав­ляя эти значения х , у и 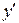в общее решение и в его производную, получим два уравнения для отыскания произвольных посто­янных и 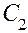. Если правая часть уравнения — функция 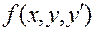— непрерывна в некоторой окрестности значений 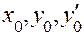и имеет там непрерывные частные производные 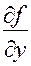и 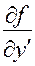то существует единственное частное решение, удовлетворяющее данным начальным условиям (теорема существования и единственности решения).

В дальнейшем особенно часто будут встречаться линей­ные дифференциальные уравнения второго порядка.

Для однородного уравнения

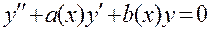
общее решение есть линейная комбинация двух его частных решений 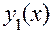и если только эти решения линейно независимы (т. е. 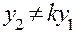где k — константа):

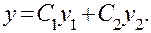
Общее решение неоднородного уравнения

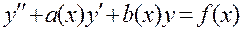
есть сумма какого-либо его частного решения и общего решения соответствующего однородного уравнения.

В этой книге будут изучаться дифференциальные урав­нения с частными производными, т. е. уравнения, содер­жащие неизвестную -функцию нескольких переменных и ее частные производные. Обычно приходится иметь дело с уравнениями для функций двух или трех независимых пе­ременных. Вот примеры таких уравнений (х, у, z— незави­симые переменные, u — неизвестная функция):

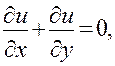
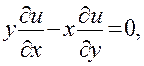
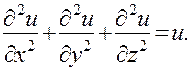
В первой строке написаны уравнения, содержащие част­ные производные только первого порядка. Такие уравнения называются уравнениями первого порядка. Соответственно уравнения, написанные во второй строчке, являются приме­рами уравнений второго порядка.

Мы вовсе не ставим перед собой задачу изучать вообще способы решений дифференциальных уравнений с частными производными. Мы будем рассматривать только те конкрет­ные уравнения (да и то далеко не все), которые сущест­венны для физики, механики и техники. Именно эти урав­нения и называются дифференциальными уравнениями ма­тематической физики.

Предварительно без доказательств познакомимся с про­стейшими свойствами уравнений с частными производными; будем считать, что неизвестная функция и зависит от двух переменных x и у.

Возьмем уравнение

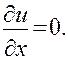
Ясно, что искомая функция и (х_, у) не зависит от переменной х, но может быть любой функцией от у:

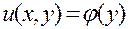, (2)

Действительно, дифференцируя функцию 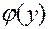поx, мы получаем нуль, а это и значит, что равенство (1) соблю­дается. Следовательно, решение (2) уравнения (1) содержит одну произвольную функцию 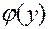. В этом и заключается коренное отличие решения уравнения с частными произ­водными первого порядка от общего решения обыкновен­ного дифференциального уравнения первого порядка, кото­рое содержит лишь произвольную постоянную. По аналогии решение (2), содержащее одну произвольную функцию, будем называть общим решением уравнения (1). Рассмотрим более сложное уравнение

(3)

где f(у) — заданная функция. Все функции и (х, у), удо­влетворяющие уравнению (3), имеют вид

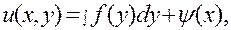(4)

где 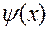— произвольная функция от х . Это можно проверить, дифференцируя обе части равенства (4) по у. Найденное решение уравнения (3) зависит от одной произвольной функ­ции, т. е. является общим.

Легко проверить, что уравнение 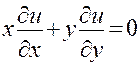имеет общее решени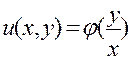е , где 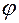— произвольная диф­ференцируемая функция.

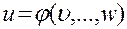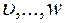Напомним для этого правило дифференцирования слож­ной функции нескольких переменных (см. [1], п. 116). Если где — функции переменных 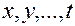то

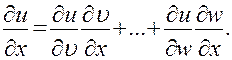
Аналогичные формулы имеют место и для производных по 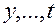. При этом число промежуточных аргументов 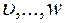, так же как и число независимых переменных 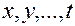может быть любым.

В нашем пример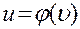е , где 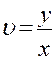. Поэтому

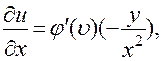
Подставляя эти выражения в уравнение, получим тождество

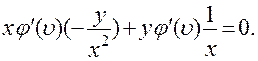
Точно так же можно проверить, что уравнение 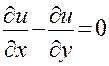имеет общее решение 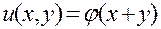, а урав­нение 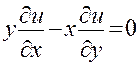имеет общее решение 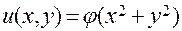, где — 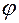произвольная дифференцируемая функция.

Рассмотрим теперь уравнения второго порядка. Пусть

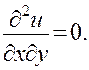(5)

Положим 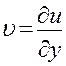. Тогда уравнение (5) примет вид . Общим решением уравнения 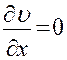бу­дет произвольная функция f (у). Возвращаясь к функции u, получим опять уравнение первого порядка

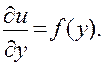
Согласно (4) его общим решением будет функция

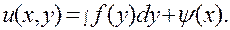
Так как 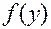— произвольная функция от у, то и инте­грал от нее также является произвольной функцией, которую мы обозначим через 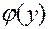. В результате мы получили реше­ние в виде

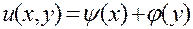, (6)

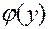где и 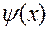— произвольные дифференцируемые функции. Легко проверить, что функция (6) действительно удовлет­воряет уравнению (5).

Решение (6) уравнения (5) с частными производным вто­рого порядка содержит уже две произвольные функции. В этом случае оно называется общим решением.

Проверим, что функция является общим решением уравнения

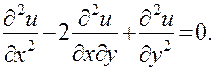
Пользуясь приведенным выше правилом дифференцирования сложной функции и обозначая , последовательно получим:

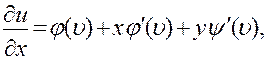
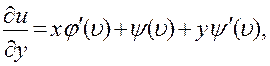
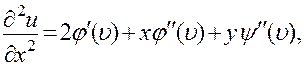
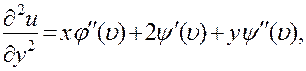
Подставляя выражения для производных в левую часть урав­нения, убеждаемся, что она обращается в нуль.

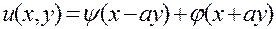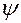Предлагаем читателю проверить, что функция , где и 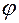— произвольные дважды дифференцируемые функции, является общим решением урав­нения 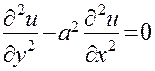, а функция 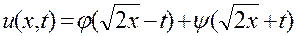— общим решением уравнения

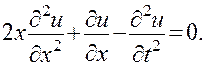
До сих пор мы еще не ставили вопроса об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т. е. функцию, удовлетво­ряющую как дифференциальному уравнению, так и дополнительным условиям.

Оказывается, что дифференциальные уравнения математической физики, которыми мы будем в дальнейшем заниматься, имеют между собой довольно много общих черт: все они — второго порядка и линейны относительно неизвест­ной функции и ее частных производных. Чаще всего все ко­эффициенты перед функцией и ее производными — постоян­ные числа. Общий вид таких уравнений для функции u, за­висящей от двух переменных х и у, таков:

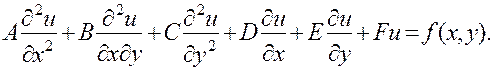(7)

где А, В, С, D, Е и F — постоянные числа, а правая часть — заданная функция переменных х и у.

Отметим, что характер и поведение решений этого урав­нения существенно зависят от его коэффициентов. Об этом мы скажем в заключении, после того как познакомим­ся с простейшими уравнениями типа (7) и способами их решений.{Отчасти порядок изложения материала в книге будет напо­минать порядок изложения теории кривых второго порядка в курсе аналитической геометрии. Там тоже вначале пишут общее уравне­ние кривых второго порядка 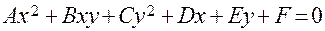— а исследование его производят лишь после изучения свойств эл­липса, параболы и гиперболы, т. е. кривых, уравнения которых представляют частные виды общего уравнения. Эта аналогия, как мы увидим в заключении, не случайна, она служит основанием для классификации уравнений типа (7).}

2. Однородные линейные дифференциальные уравнения с частными производными и свойства их решений. Если в уравнении (7) правая часть равна нулю, то уравнение на­зывается однородным. Оно имеет вид

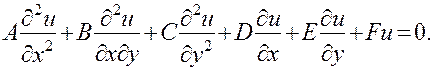(8)

Вообще в теории дифференциальных уравнений уравне­ние называется однородным, если функция, тождественно равная нулю ( 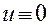) , является его решением. Решения ли­нейных однородных уравнений вида (8) обладают следующим свойством:

Если каждая из функций 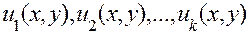является решением уравнения (8), то и их линейная комбинация

(9)

где 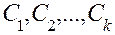— произвольные постоянные, также является решением этого уравнения.

Для доказательства достаточно заметить, что если и есть линейная комбинация частных решений:

(для краткости аргументы функций не пишутся), то любая производная функции и будет такой же линейной комбина­цией соответствующих производных функций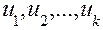

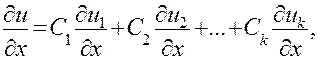
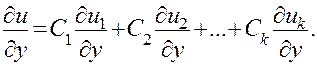
Разумеется, так же будут выглядеть и производные вто­рого порядка. Если подставить выражения для производных функций в левую часть уравнения (8) и перегруппировать слагаемые, то получим

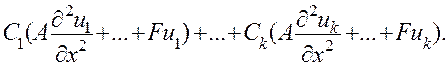
Поскольку по условию функции 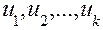являются ре­шениями уравнения (8), то каждая из скобок обратится и нуль, а вместе с ними и вся левая часть уравнения; это и означает, что функция и является его решением.

Точно такое же свойство, как известно, имеет место и для обыкновенных линейных дифференциальных уравнений. Однако надо иметь в виду, что обыкновенное линейное диф­ференциальное уравнение n-го порядка имеет в точности n линейно независимых частных решений, линейная комбинация которых и дает общее решение.

Уравнение же в частных производных может иметь, как мы убедимся в дальнейшем, бесконечное множество ли­нейно независимых частных решений, т. е. такое мно­жество решений, любое конечное число которых является функциями линейно независимыми. (Система функций 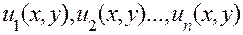называется линейно независимой, если ни одна из этих функций не является линейной комбинацией опальных.) В соответствии с этим нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с р яд а м и, членами которых служат произве­дения произвольных постоянных на частные решения:

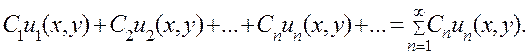(10)

Мы дадим здесь необходимые определения и укажем некото­рые свойства рядов, членами которых являются функции не­скольких переменных. Этими свойствами мы будем пользо­ваться и в дальнейшем.

Будем считать, что члены ряда — функции двух перемен­ных; все определения легко переносятся на случай функций трех переменных.

Рассмотрим функциональный ряд

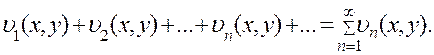(11)

Этот ряд называется сходящимся в точке 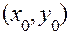, если числовой ряд 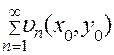сходится. Совокупность всех точек, в которых ряд сходится, называется областью сходимости ряда. Все члены ряда считаются непрерывными и дифференцируемыми функциями переменных х и у во всей области сходимости ряда.

Мы будем в дальнейшем рассматривать только такие ряды, суммы которых есть непрерывные функцииот х и у,

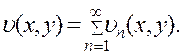(2)

Кроме того, будем предполагать, что все встречающиеся ряды можно дважды почленно дифференцировать, т. е. что

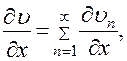
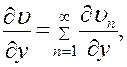
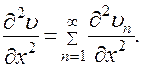(13)

и т.д.

Очень часто нам придется интегрировать ряд (12) либо по некоторой области D, либо по одной из переменных. По­следнее означает, что мы полагаем, например 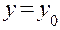и ин­тегрируем по х в некоторых пределах от 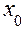до 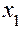. Возмож­ность почленного интегрирования ряда заключается в том, что

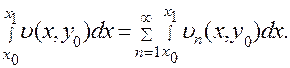(14)

(Разумеется, предполагается, что рассматриваемые значе­ния х и 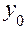принадлежат области сходимости ряда.)

Обозначим сумму ряда (10) через 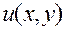и будем считать, что выполняются все введенные предположения. Тогда

Отсюда ясно, что функция 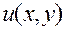—сумма ряда (10), так же как и члены ряда, является решением уравнения (8).

Можно указать сравнительно простые признаки, при соблюде­нии которых все высказанные предположения о рядах будут спра­ведливы. Введем для этого следующее определение.

Функциональный ряд

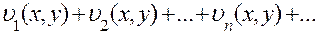
называется правильно сходящимся в области D, принадлежа­щей области сходимости ряда, если все члены его по абсолют­ной величине не превосходят соответствующих членов некото­рого сходящегося знакоположительного числового ряда, т. е.

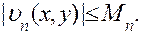
причем неравенство соблюдается во всех точках области D, а 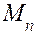— член сходящегося числового ряда.

Для правильно сходящихся рядов имеют место следующие тео­ремы, которые мы приводим без доказательства.

1. Сумма правильно сходящегося ряда из непрерывных функ­ций есть функция непрерывная.

2. Правильно сходящийся ряд можно почленно интегриро­вать.

3. Если ряды, составленные из производных сходящегося ряда, сходятся правильно, то ряд можно почленно дифферен­цировать.

Определение правильно сходящегося ряда без всяких измене­ний переносится как на функции одной переменной, так и на функ­ции трех и большего числа переменных.

Напомним, что все три сформулированные свойства имели место для степенных рядов 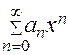в интервале их сходимости. Нетрудно показать, что степенной ряд является правильно сходя­щимся в любом интервале, целиком заключенном в интервале схо­димости ряда (см. [1], п. 190). { Для читателей, знакомых с определением равномерной схо­димости ряда, отметим, что если ряд сходится правильно, то он сходится и равномерно; однако не всякий равномерно сходящийся ряд сходится правильно.}

В дальнейшем нам встретятся и такие случаи, когда функ­ция 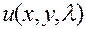при всех значениях параметра 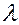, заключен­ных в некотором интервале 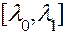, является решением урав­нения (8). Тогда говорят, что частные решения зависят от непрерывно изменяющегося параметра. Обычно ин­тервал изменения параметра 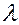составляет или всю числовую ось, или положительную полуось.

Мы будем в дальнейшем функцию 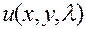записывать в виде 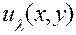. Этой формой записи подчеркивается анало­гия между случаями, когда решения зависят от параметра, принимающего только целые значения ( 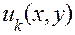), и когда решения зависят от параметра, принимающего любые значения( ).

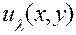Покажем, что если мы умножим функцию 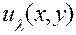на произвольную функцию С( 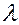) и проинтегрируем в пределах изменения параметра :

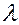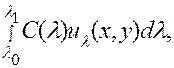(15)

то вновь получим решение уравнения (8). Ясно, что инте­грал (15) есть некоторая функция переменных х и у.

Предварительно познакомимся с некоторыми свойствами интегралов типа (15). Пусть дан интеграл

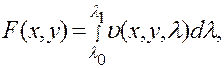(16)

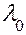где и 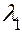— конечные пределы. Имеет место следующая теорема, которую мы приводим без доказательства.

Если подынтегральная функция , а также ее частные производные по х и по у непрерывна при всех рассматриваемых значениях аргументов х, у и 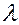то и функция F(x, у) непрерывна вместе со своими частными производными, причем

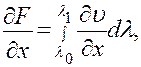
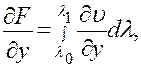
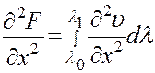(17)

и т. д.

В случае, когда хотя бы один из пределов интегриро­вания обращается в бесконечность, интеграл (16) ста­новится несобственным и указанные свойства функции F(x, y) соблюдаются лишь при некоторых дополнительных условиях, о которых мы скажем ниже.

Возвращаясь к интегралу (15), обозначим его через U(x, у) и предположим, что для него справедливы фор­мулы (17). При этом пределы интегрирования 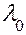и 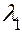могут быть как конечными, так и бесконечными. Тогда

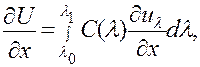
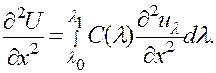
и т. д.

Подставляя выражения для функции U(x, у) и ее про­изводных в уравнение (8) и заменяя сумму интегралов ин­тегралом от суммы функций, получим в левой части

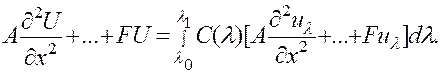
Так как по предположению выражение в квадратных скобках при любом 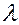равно нулю (ведь функция 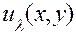при любом 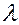является решением уравнения (8)), то и весь интеграл равен нулю. Следовательно, функция U (x, у) дей­ствительно является решением уравнения.

Сформулируем простой признак, аналогичный соответствую­щему признаку для рядов, при соблюдении которого выполняются все приведенные свойства для несобственных интегралов вида 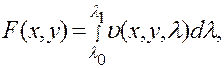где один или оба предела интегрирова­ния обращаются в бесконечность.

Если можно указать такую положительную функцию , что для всех рассматриваемых значений х, у и 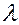соблюдается неравенство 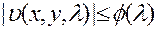и несобственный интеграл от функции сходится, то функция F(x, у) непрерывна. Такую сходимость несобственного интеграла от функции будем называть правильной.

Если аналогичное свойство имеет место и для интегралов от частных производных функции , то функция F (х, у) дифференцируема и ее производные находятся по формулам (17). Например, если — и интеграл от 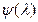сходится, то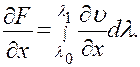

3. Оператор Лапласа в полярных, цилиндрических и сферических координатах. { Этот пункт следует прочесть или перед изучением задач, в которых встретится необходимость преобразования оператора Лапласа (п. 32, п. 49—50), или перед чтением гл. III } В этом пункте мы рассмо­трим вспомогательный вопрос о выражении оператора Лап­ласа о различных системах координат; эти выражения пона­добятся нам в дальнейшем. Напомним, что трехмерным оператором Лапласа 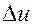называется выражение

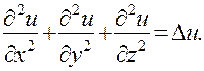(18)

где — функция трех переменных. Если функция и зависит только от двух переменных, то оператор Лапласа

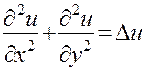(19)

называется двумерным.

Начнем с двумерного оператора Лапласа и произведем замену декартовых координат х и у полярными r и 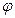по формулам

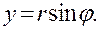(20)

Если в функцию 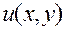подставить вместо x и у их выражения, то получится функция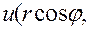 перемен­ных r и 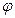. Выразив вторые производные от функции u по х и по у через производные по r и 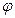и подставив затем найденные выражения в формулу (19), мы и получим опера­тор Лапласа в полярных координатах.

По правилу дифференцирования сложной функции

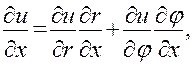
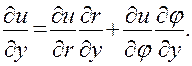(21)

Для отыскания частных производных r и 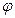по х и у выразим из формул (20) r и 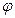. Находим, что 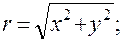отсюда

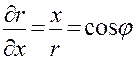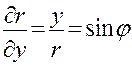и (22)

Поскольку 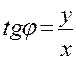, то

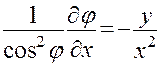и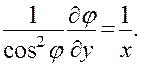

Заменяях и у по формулам (20), получим

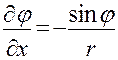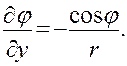и (23)

Подставив (22) и (23) в равенства (21), окончательно найдем выражения частных производных 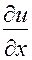и 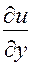через пере­менные r и 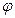и производные по этим переменным:

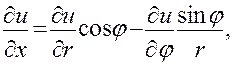
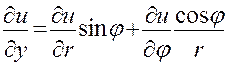(24)

Перейдем к отысканию вторых производных. Применим к производной 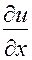опять правило дифференцирования слож­ной функции

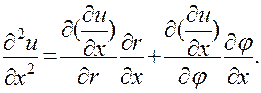
Из равенств (24) ^д{дї) д*и

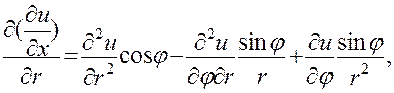
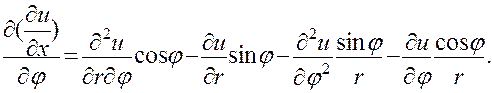
Умножим теперь первое равенство на 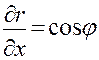, а второе на 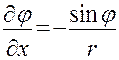и сложим. Приводя подобные члены, по­лучим

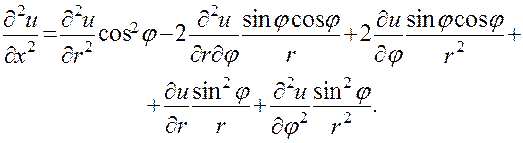(25)

Совершенно аналогично, воспользовавшись соотношением

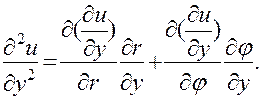
найдем, что

(26)

Складывая (25) и (26), окончательно получим выражение оператора Лапласа в полярных координатах:

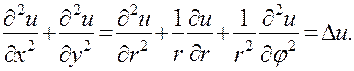(27)

Последнее выражение очень часто бывает удобно запи­сать в следующем виде:

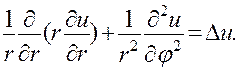(28)

Тождественность правых частей формул (28) и (27) легко проверяется дифференцированием.

Перейдем к трехмерному случаю и начнем с цилин­дрических координат. Цилиндрические координаты r , 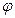иz связаны с декартовыми соотношениями

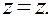
Функция преобразуется в функцию 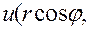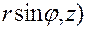. Здесь третья переменная z остается неизменной, и в выражении (27) двумерного оператора Лапласа в поляр­ных координатах добавляется только вторая производная по z:

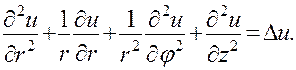(29)

Для сферических координат r , 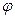и 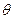имеем формулы:

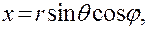
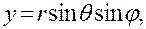
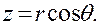
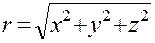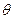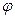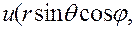
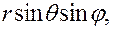
в которых — расстояние точки (х, у, z) от начала координат, — угол между радиусом-вектором точки и осью Oz, а — угол между проекцией радиуса- вектора на плоскость Оху и осью Ох. Здесь непосредствен­ное преобразование производных функции 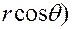очень громоздко, и мы его проводить не будем, ограничившись тем, что выпишем окончательное выражение оператора Лапласа в сферических координатах:

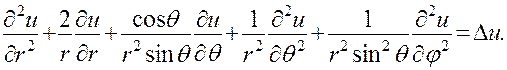
Эту формулу часто записывают в виде

(31)

Предоставляем читателю проверить тождественность обеих формул.