Классификация линейных дифференциальных урав­нений с частными производными второю порядка.

Общий вид линейного диффе­ренциального уравнения второго порядка при условии, что неизвестная функция u зависит от двух переменных x и y, таков:

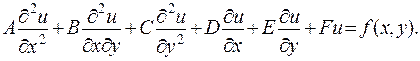(1)

Предполагаем, что все коэффициенты уравнения постоянны {Приводимая ниже классификация линейных уравнений пере­носится и на уравнения с переменными коэффициентами, которые здесь не рассматриваются}.

Большинство дифференциальных уравнений второго порядка математиче­ской физики пред­ставляют частные случаи общего уравнения (1).

Так, если для единообразия обозначений вместо пере­менной t (времени) писать переменную y, то уравнение сво­бодных колебаний струны (§ 1) примет вид

(2)

a уравнение линейной задачи теплопроводности (§ 12)

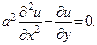(3)

Наконец, уравнение Лапласа (§18) в двумерном случае имеет вид

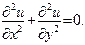(4)

В уравнении (4) обе вторые частные производные входят в левую часть с одинаковыми знаками, в уравнении (2) — с противоположными знаками, а в уравнении (3)—вторая производная по одной из переменных вовсе не входит.

Л. Эйлер доказал, что любое дифференциальное урав­нение вида (1) с помощью замены независимых переменных x и y может быть приведено к одному из следующих трех видов.

1. Если то после введения новых незави­симых переменных и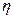

{мы ограничимся только принципиальной стороной вопроса и не указывая формул, по которым фактически производится замена переменной } уравнение (1) примет вид

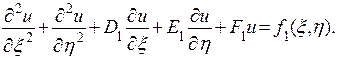(5)

В этом случае уравнение называется эллиптическим. Наи­более простым эллиптическим уравнением является уравнение Лапласа (4).

2. Если 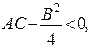то уравнению (1) можно при­дать вид

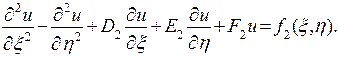(6)

Такое уравнение называется гиперболическим; простей­шим примером его является одномерное уравнение свободных колебаний (2).

1. Если то уравнение (1) приводится

к следующему:

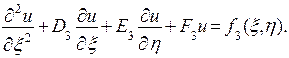(7)

и называется параболическим. Примером его служит урав­нение линейный теплопроводности (3).

Наименования уравнений объясняются тем, что при исследовании общего уравнения кривых второго порядка 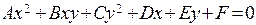оказывается, что в случае 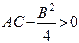кривая представляет эллипс, в случае 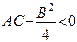— гиперболу и в случае 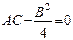- параболу.

{Поскольку бывают еще случаи вырождения кривых второго порядка, то чаще говорят, что в первом случае кривая эллиптического типа, во втором — гиперболического и в треть­ем— параболического (см., например, книгу Н. В. Ефимова «Квадратичные формы и матрицы», Физматгиз, М., 1967)}

Уравнения (5), (6) и (7) можно еще более упростить введением новой неизвестной функции. Именно, вводя функ­цию 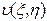по формуле

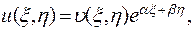(8)

мы можем всегда подобрать числа 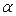и 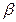так, что в эллипти­ческом и гиперболическом уравнениях исчезнут члены с про­изводными первого порядка, а в параболическом — член с первой производной по одной из независимых переменных (в уравнении (7) по 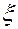) и член с самой функцией.

Введение вспомогательной функции по формуле (8) уже встречалось нам в п. 21 при изучении телеграфного уравнения для линии без искажений (см. формулу (7.13)).

Окончательно любое уравнение вида (1) может быть, с учетом сделанных замечаний, приведено к одному из сле­дующих канонических типов:

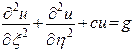(эллиптический тип),

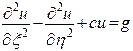(гиперболический тип),

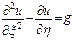(параболический тип)

(с—постоянное число, g — функция переменных х и у).

69. Корректность постановки задач математической физики.

Уравнения гиперболического и параболического типов возникают чаще всего при изучении процессов, про­текающих во времени (это были колебаний, распространения электрических волн, распростра­нения тепла, диффузии). В одномерном случае всегда уча­ствовала одна координата х и время t.

Поэтому канонические уравнения этих типов обычно за­писываются так:

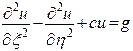(гиперболический тип),

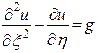(параболический тип).

Для задач, приводящих к таким уравнениям, дополни­тельные условия разделяются на начальные и краевые.

Начальные условия, как мы видели, состоят в задании при t = 0 значений искомой функции u и ее про­изводной (в гиперболическом случае) или только значений самой функции (в параболическом случае).

Краевые условия для этих задач заключаются в том, что указываются значения неизвестной функции u(x, t) на концах интервала изменения координаты (в задаче о коле­баниях струны эго концы струны {в задаче о колебаниях мембраны задаются значения неиз­вестной функции на контуре мембраны}, в задаче о распростра­нении электрических колебаний это концы линии, в задаче о линейной теплопроводности это концы стержня и т. д.) .

Если процесс протекает в бесконечном интервале изменения координаты х (бесконечная струна, бесконечный стержень), то краевые условия отпадают и получается за­дача только с начальными условиями, или, как ее часто называют, задача Коши.

Если ставится задача для конечного интервала, то должны быть заданы и начальные и краевые условия. Тогда говорят о смешанной задаче.

Уравнения эллиптического типа возникают обычно при исследовании стационарных процессов. Время t в эти уравнения не входит, и обе независимые переменные являются координатами точки. Такими оказываются уравнения стацио­нарного температурного поля, электростатического поля и уравнения многих других физических задач.

Для задач такого типа ставятся только краевые усло­вия, т. е. указывается поведение неизвестной функции на контуре области. Это может быть задача Дирихле, когда заданы значения самой функции; задача Неймана, когда заданы значения нормальной производной искомой функции, и, наконец, задача, когда на контуре задана линейная комбинация функции и ее нормальной производной.

В основных задачах математической физики, именно физические соображения подсказывают, какие дополнительные условия следует поста­вить в той или иной задаче, чтобы получить единственное ее решение, отвечающее характеру изучаемого про­цесса.