МАТЕМАТИЧЕСКИЕ МОДЕЛИ СРЕДСТВ ИЗМЕРЕНИЙ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Если вход СИ нельзя представить в виде одной точки, и он распределен по некоторой линии или поверхности, то такое СИ или систему называют СИ или системой с распределенными параметрами [34, 57]. Динамические свойства таких СИ могут быть описаны широким классом уравнений математической физики: дифференциальными уравнениями в частных производных, интегральными уравнениями, интегродифференциальными уравнениями с полными и частными производными и т. д.
По существу, большинство технических средств являются средствами с распределенными параметрами. К наиболее типичным представителям, например, СИ механических и теплофизических величии с распределенными параметрами относятся измерительные преобразователи, а, следовательно, и приборы температур, давлений и тепловых расходомеров.
До настоящего времени основное внимание уделялось исследованию и описанию систем с сосредоточенными параметрами. Это объясняется исключительно тем, что эти модели значительно проще как в описании, так и в исследовании и являются некоторым упрощением систем с распределенными параметрами. Однако возрастающие требования к точности СИ, а следовательно, и к адекватности математических моделей все чаще приводят к необходимости детального изучения именно СИ с распределенными параметрами.
О сложности динамических моделей систем с распределенными параметрами свидетельствует необходимость их описания краевыми задачами с граничными и начальными условиями. При этом подходы к описанию, а, следовательно, математические модели и их исследование весьма разнообразны и, как правило, связаны с конкретной задачей. Однако имеется и ряд обобщений. Например [58], для описания и расчета механических систем используется матричный метод начальных параметров, позволяющий преобразовать исследование сложной механической системы в цикл алгебраических операций.
В справочном пособии [57] приведены около 500 краевых задач, разбитых на отдельные непересекающиеся группы. При этом предлагается использование [57, 58] структурного метода исследования систем с распределенными параметрами, который вообще говоря, является обобщением структурного метода (п. 4.2) для СИ с сосредоточенными параметрами. Обобщение математических моделей некоторых типов ИМ [34] температуры, давления и других, и методов их анализа не противоречит идее и основным положениям структурного метода. Но основное внимание уделено математическим моделям в виде дифференциальных и интегральных уравнений.
В данной лекции рассмотрим лишь сущность структурного метода описания и исследования СИ с распределенными параметрами, описание динамических свойств в виде дифференциальных уравнений и основные динамические характеристики этих средств.
В основе структурного метода лежит идея распределенного блока, который соответствует физическому процессу в сплошной среде и является обобщением преобразователей или звеньев СИ с сосредоточенными параметрами.
Распределенным блоком [57] называется устройство любой природы, в котором выделены вход и выход (рис. 4.19), причем на вход поступает входной распределенный сигнал V (х, t), а на выходе появляется выходной, также распределенный сигнал U (х,t), 
который, однако, может иметь и другую размерность. Распределенный блок или преобразовательный элемент, как и в случае СИ с сосредоточенными параметрами, позволяет представить средство измерений в виде структурной схемы с последовательным, параллельным и встречно-параллельным соединениями этих элементов. Это позволяет [57], используя правила преобразования, суммирования и вычитания распределенных сигналов и имея математические модели отдельных элементов, получить математическую модель СИ с распределенными параметрами.
Распределенным [57], или многомерным [34], сигналом называется функция f(х,t), 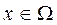 ,
, 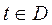 , где х — пространственная переменная;
, где х — пространственная переменная; 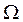 — область в r-мерном евклидовом пространстве
— область в r-мерном евклидовом пространстве 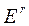 ; D — область числовой оси.
; D — область числовой оси.
Если в распределенном сигнале f (х, t), 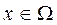 , размерность пространственной области
, размерность пространственной области 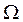 есть r, то сигнал называется r-мерным распределенным сигналом.
есть r, то сигнал называется r-мерным распределенным сигналом.
Рассмотрим определения для некоторых частных случаев распределенного сигнала. Если функция f (х, t) принимает числовые значения, то сигнал называется скалярным. Если в качестве функционального пространства сигналов рассматриваются функции f, независящие от пространственной переменной х, а зависящие только от переменной t, то сигналы f(t) называют сосредоточенными. Если рассматриваются функции f, зависящие только от переменной х, то сигналы f (х) называют статическими распределенными.
Для исследования систем с распределенными параметрами вводится понятие многомерной 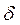 -функции. Эта функция обладает теми же свойствами и значением, как и
-функции. Эта функция обладает теми же свойствами и значением, как и 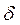 -функция, рассмотренная ранее (п. 2.2) для систем с сосредоточенными параметрами.
-функция, рассмотренная ранее (п. 2.2) для систем с сосредоточенными параметрами.
Так, например, четырехмерная 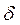 -функция (одна временная и три пространственные координаты)
-функция (одна временная и три пространственные координаты)
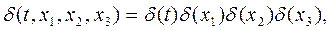 (4.136)
(4.136)
или
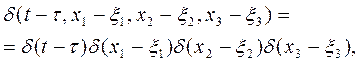 (4.137)
(4.137)
где 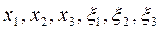 — декартовы координаты некоторой точки М и М0.
— декартовы координаты некоторой точки М и М0.
Также справедливо интегральное свойство
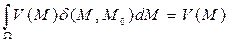 (4.138)
(4.138)
где V (M) — непрерывная функция в точке М0.
Динамика СИ с распределенными параметрами может быть описана дифференциальным уравнением [34, 57, 58]
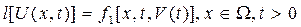 (4.139)
(4.139)
с граничным
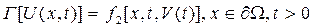 (4.140)
(4.140)
и начальным условиями
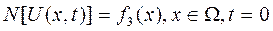 (4.141)
(4.141)
где l, Г, N — линейные дифференциальные операторы основного уравнения (4.139), граничных (4.140) и начальных (4.141) условий;  — граница области
— граница области 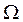 .
.
Так как возможно существование некоторой функции  линейно зависящей от
линейно зависящей от 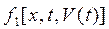 ,
, 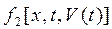 и
и  , то уравнения (4.139) ... (4.141) могут быть приведены к эквивалентным с однородными граничными и нулевыми начальными условиями:
, то уравнения (4.139) ... (4.141) могут быть приведены к эквивалентным с однородными граничными и нулевыми начальными условиями:
 (4.142)
(4.142)
 (4.143)
(4.143)
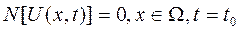 (4.144)
(4.144)
Импульсная характеристика 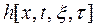 для СИ с распределенными параметрами будет функцией четырех переменных — двух временных
для СИ с распределенными параметрами будет функцией четырех переменных — двух временных 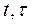 и двух пространственных — и является решением краевой задачи (4.142) ... (4.144) при
и двух пространственных — и является решением краевой задачи (4.142) ... (4.144) при
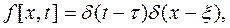
то есть
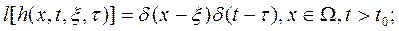 (4.145)
(4.145)
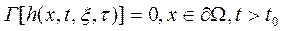 (4.146)
(4.146)
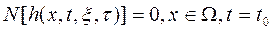 (4-147)
(4-147)
Зная импульсную характеристику, можно найти решение задачи (4.139) ... (4.141) при произвольных начальных условиях:
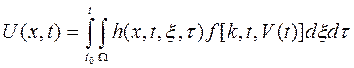 (4.148)
(4.148)
Для случая, если задача не зависит от пространственной переменной х, выпадают граничные условия (4.143) или (4.146), а импульсная характеристика 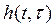 удовлетворяет уравнениям
удовлетворяет уравнениям
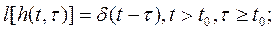 (4.149)
(4.149)
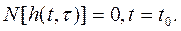 (4.150)
(4.150)
Решение задачи при произвольных 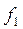 и f3:
и f3:
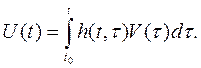 (4 151)
(4 151)
Для стационарных СИ импульсная характеристика будет зависеть только от трех аргументов — 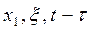 , так как уравнения (4.142) ... (4.144) инвариантны к сдвигу во времени. В этом случае
, так как уравнения (4.142) ... (4.144) инвариантны к сдвигу во времени. В этом случае
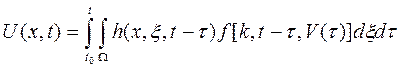 (4.152)
(4.152)
Для СИ с распределенными параметрами также, как и для средств с сосредоточенными параметрами, можно воспользоваться понятием единичной переходной функции 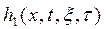 , которая будет представлять собой реакцию невозбужденного СИ на единичный ступенчатый распределенный сигнал.
, которая будет представлять собой реакцию невозбужденного СИ на единичный ступенчатый распределенный сигнал.
Следует заметить, что для СИ с распределенными параметрами за выходные сигналы, как правило, принимаются некоторые усредненные по пространству значения входного сигнала, распределенного в чувствительном элементе [34]. Поэтому часто удается, во-первых, упростить задачу, считая при этом 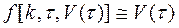 . В этом случае выходной сигнал стационарного СИ может быть представлен в виде
. В этом случае выходной сигнал стационарного СИ может быть представлен в виде
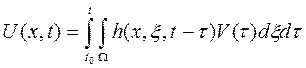 (4.153)
(4.153)
Во-вторых, если выходной сигнал СИ является некоторым функционалом от локальной реакции 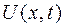 , то соотношение (4.153) целесообразно привести к виду
, то соотношение (4.153) целесообразно привести к виду
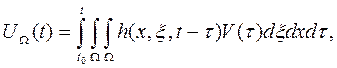 (4.154)
(4.154)
называемому интегральной реакцией СИ с распределенными параметрами.
Передаточная функция, согласно определению для стационарной задачи, может быть получена преобразованием Лапласа во времени от импульсной характеристики 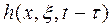 :
:
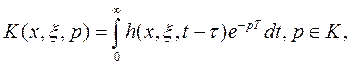 (4.155)
(4.155)
где 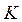 — поле комплексных чисел.
— поле комплексных чисел.
Локальная передаточная функция может быть получена также с применением преобразований Лапласа к уравнениям задачи [34] при нулевых начальных условиях:
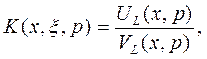 (4.156)
(4.156)
и представляет собой дробно-рациональную функцию.
Частотная передаточная функция или характеристика аналогично (4.155) получается преобразованием Фурье от импульсной характеристики:
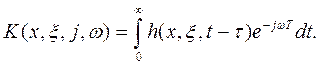 (4.157)
(4.157)
Таким образом, СИ с распределенными параметрами (как и СИ с сосредоточенными параметрами) могут быть описаны дифференциальными уравнениями, передаточной и частотной передаточной функциями.
В качестве примера приведем математическую модель манометра с упругим чувствительным элементом без учета влияния аэродинамических трасс. Его динамические свойства, как средства с распределенными параметрами в декартовых координатах, описываются краевой задачей
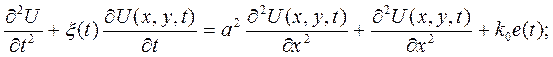 (4.158)
(4.158)
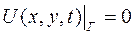 (4.159)
(4.159)
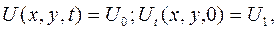 (4.160)
(4.160)
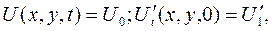 (4.160)
(4.160)
где 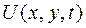 — отклонение точки
— отклонение точки 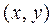 мембраны от положения равновесия; а — величина, характеризующая отношение натяжения к поверхностной плотности;
мембраны от положения равновесия; а — величина, характеризующая отношение натяжения к поверхностной плотности; 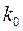 — величина, обратная поверхностной плотности мембраны;
— величина, обратная поверхностной плотности мембраны;  — отношение коэффициента затухания от вязкого трения к массе мембраны.
— отношение коэффициента затухания от вязкого трения к массе мембраны.
Аналогично уравнения могут быть представлены в полярных координатах.
Если учитывать течение в аэродинамической трассе (подводные трубки и полость мембранной коробки), то давление р (t) в уравнении (4.158) следует рассматривать как входной сигнал другой системы, являющейся также распределенной и описываемой краевой задачей. В этом случае динамические свойства СИ будут описываться уже системой дифференциальных уравнений в частных производных.
Для составления уравнений (4.158) ... (4.160) можно, например, воспользоваться физическими явлениями и законами [59] или уравнениями Лагранжа [60]. В основу методов составления математической модели СИ с распределенными параметрами могут быть положены методы, рассмотренные для СИ с сосредоточенными параметрами. Однако при этом они значительно усложняются в связи с необходимостью учета пространственного распределения сигнала и физических явлений в процессе его преобразования.
Представить здесь все разнообразие и пути составления математических моделей СИ с распределенными параметрами не представляется возможным. Поэтому воспользуемся обобщениями математических моделей [34, 57] и рассмотрим несколько типов обобщенных моделей, к которым могут быть приведены многие ИП- преобразователи для измерений температуры контактным методом, задача описания которых сведена к описанию систем в виде неограниченной пластины, шара или неограниченного цилиндра; пленочные термоприемники; измерительные преобразователи давлений и др.
В качестве типовых математических моделей ИП могут быть приняты параболическая и гиперболическая линейные модели [34].
К точным методам анализа [34, 50] могут быть отнесены: метод разделения переменных, использование преобразований Лапласа, методы конечных интегральных преобразований и др.
Рассмотрим этот вопрос на примере метода разделения переменных, который является одним из эффективных методов решения краевых задач. Его еще называют методом Фурье, или методом собственных функций.
МЕТОД ФУРЬЕ, ИЛИ МЕТОД СОБСТВЕННЫХ ФУНКЦИЙ.
Основная идея метода заключается в том, что решение краевой задачи в частных производных сводится к решению вспомогательных уравнений или дифференциальных уравнений в частных производных, но с меньшим числом независимых переменных. При этом решение уравнения в частных производных строится в виде произведений (суммы) из решений вспомогательных краевых задач. Затем из этих решений в виде линейной комбинации с постоянными коэффициентами находится решение первоначальной краевой задачи.
Решение дифференциального уравнения в частных производных можно искать в виде
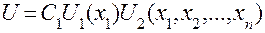 (5.16)
(5.16)
или
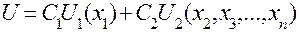 (5.17)
(5.17)
Если после подстановки предполагаемого решения исходное уравнение можно записать в виде
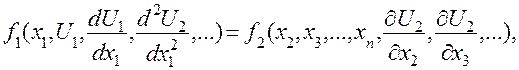 (5.18)
(5.18)
то, так как это соотношение должно быть справедливым при любых значениях времени и пространственных координат, левая и правая части его равны некоторой постоянной величине b:
 (5.19)
(5.19)
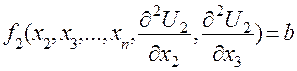 (5.20)
(5.20)
где b — произвольная постоянная, определяемая из начальных условий.
Уравнение (5.19) является при этом обыкновенным дифференциальным уравнением с одной переменной, а уравнение (5.20) содержит на одну переменную меньше. Таким образом, задача сведена к решению двух уравнений. Для уравнения второго порядка
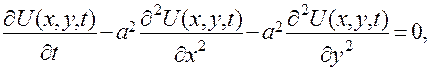 (5.21)
(5.21)
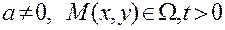
с некоторыми начальными и граничными условиями частное решение может быть найдено в виде (5.16)
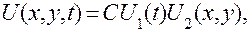 (5.22)
(5.22)
где С — произвольная постоянная;  — временная функция;
— временная функция; 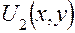 — функция только пространственных координат. Подставив (5.22) в (5.21), получим
— функция только пространственных координат. Подставив (5.22) в (5.21), получим
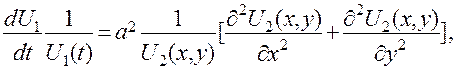 (5.23)
(5.23)
или
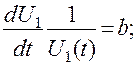
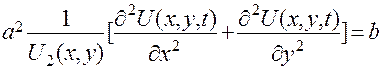 (524)
(524)
Решение уравнения для  может быть записано в виде
может быть записано в виде  если постоянную интегрирования отнести к С. Теперь воспользуемся тем, что после воздействия на вход реального СИ при
если постоянную интегрирования отнести к С. Теперь воспользуемся тем, что после воздействия на вход реального СИ при  на его выходе должен быть установившийся процесс, то есть величина b должна быть отрицательной. Тогда, положив
на его выходе должен быть установившийся процесс, то есть величина b должна быть отрицательной. Тогда, положив 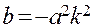 , где k — некоторая пока неизвестная постоянная, (5.23) можно представить в виде
, где k — некоторая пока неизвестная постоянная, (5.23) можно представить в виде
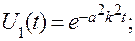 (5.25)
(5.25)
 (5 26)
(5 26)
Отыскав решение однородного дифференциального уравнения (5.26), соответствующее 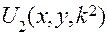 (как отыскивается здесь опущено), частное решение исходного уравнения в соответствии с (5.22) и (5.25):
(как отыскивается здесь опущено), частное решение исходного уравнения в соответствии с (5.22) и (5.25):
 (5.27)
(5.27)
Поскольку 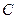 и
и 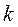 могут принимать различные значения, то будет множество частных решений, то есть
могут принимать различные значения, то будет множество частных решений, то есть
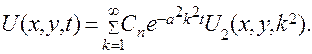 (5.28)
(5.28)
Постоянные  определяются изначальных условий, а
определяются изначальных условий, а  – из граничных.
– из граничных.
(До этого места материал брался из книги Таланчука, Рущенко, а далее из книги Арамановича, Левина.)
Дата добавления: 2015-11-18; просмотров: 1218;
