Использование MS Excel для решения финансовых и экономических задач
Статистические функции, прогнозирование динамических рядов
Краткая характеристика проблемы
Один из наиболее распространенных методов прогнозирования заключается в экстраполяции, т.е. в продлении в будущее тенденции, наблюдавшейся в прошлом. С помощью Excel можно анализировать тренды и делать прогнозы. Линии тренда показывают тенденцию изменения данных и используются для составления прогнозов. Для создания линии тренда на основе данных диаграммы применяется та или иная аппроксимация.
Линии тренда – статистический инструмент, и они, как и любой другой статистический инструмент, могут быть ошибочно или неправильно использованы. Для того, чтобы правильно применять линии тренда для анализа данных на диаграмме и, чтобы они действительно представляли тренд отображаемых на диаграмме данных, необходимо хорошо разбираться в теоретических основах. Теоретические основы регрессионного анализа кратко изложены в разделе 3 настоящего практикума. Для более детального изучения этих вопросов следует обратиться к специальной литературе по статистике.
Если в регрессии можно считать время в качестве независимой переменной, то ход развития явления, процесса связывается не с какими-либо конкретными факторами, а с течением времени (а точнее с временным интервалом: сек., мин., час, сут., неделя, мес., квартал, год,). В таком случае терминология "Регрессионный анализ" заменяется на – "Анализ временных рядов". Например, в торгах на Международных валютных биржах динамика изменения цен в реальном режиме определяется секундами.
ЗАДАНИЕ
Имеется следующая информация предприятияю торговли о продолжительности эксплуатации типового оборудования и затратах на его ремонт(табл. 1).
В целях нормирования расхода средств на ремонт оборудования найти зависимость затрат на ремонт оборудования от срока эксплуатации оборудования.
Таблица 1
| Срок эксплуатации оборудования (лет) Xi | Затраты на ремонт (тыс. руб.) Yi |
При статистическом изучении связи показателей выберем прямолинейную форму зависимости (аппроксимации) между признаками Х и Уприменением формулы У =А0 + A1 * X.
1. Построить линейный тренд для данных таблицы 3.
Действия:
· Ввести значения Х и У по образцу(рис. 1).
· Щелкнуть на пиктограммеМастера диаграмм 
 . Выбрать тип диаграммыЛинейная (Excel 95) илиТочечная (Excel 97).
. Выбрать тип диаграммыЛинейная (Excel 95) илиТочечная (Excel 97).
· Ввести названия диаграммы и осей по образцу .
· Закончить построение диаграммы;
· Выбрать команду главного менюДиаграмма, Добавить линию тренда (Excel 97) или –Вставка, Линия тренда. Выбрать тип тренда –линейный;
· Раскрыть вкладкуПараметры и установить опцию –Прогноз на 1 период вперед, затем установить флажок –показывать уравнение на диаграмме, и флажок –поместить на диаграмму величину достоверности аппроксимации R2). Щелкнуть на кнопкеОК.
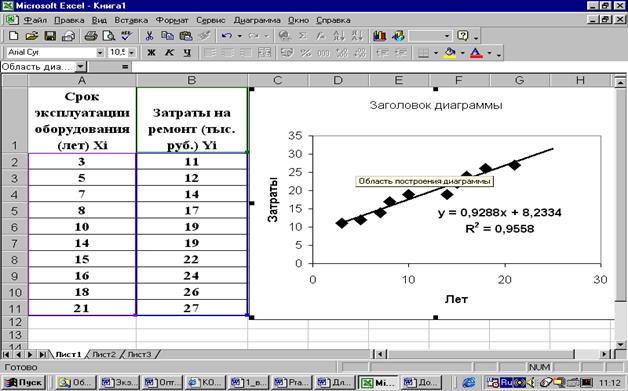
Рис. 1. Вид таблицы данных и линейного тренда
2. Для числовых значений диапазона ячеекB2:B11 вычислить среднее значение и результат поместить в ячейкуB12.
Действия:
· Установить курсор в ячейкуB12, активизироватьМастер функций,щелкнув на пиктограмме  fx.
fx.
· В диалоговом окне Мастер функций [шаг 1 из 2] выбрать Категория – Статистические, Функция –СРЗНАЧ. В полеЧисло окна функции СРЗНАЧ щелкнуть на кнопке с красной стрелкой, затем выделить диапазон ячеекB2:B11 и снова щелкнуть на кнопке с красной стрелкой в поле функции, затем щелкнуть на кнопке ОК. В ячейкеС16 появится среднее значение – 19,1.
3. Для числового ряда из диапазона ячеекB2:B11 аналогично вычислитьмаксимальное и минимальное значения
Введение
Чтобы лучше представить, о чем идет речь, рассмотрим задачу, имеющее очевидное решение. Предположим, что магазин торгует магнитофонами по цене 500 руб. и телевизорами по цене 2000 руб. Требуется определить, сколько нужно продавать в день магнитофонов и телевизоров, чтобы выручка была максимальной.
Очевидный ответ будет таким: как можно больше телевизоров и как можно больше магнитофонов. Реальные возможности магазина ограничены. В день можно продать не более 70 магнитофонов и не более 50 телевизоров. Значит нужно продавать именно это количество товара. Максимальная выручка составит:
500*70+2000*50=13500 руб.
Теперь перейдем к математической постановке задачи. Определим выручку В как линейную функцию двух переменных.
В=500*m+2000*t,
где переменные m и t обозначают количество магнитофонов и телевизоров.
Если в плоскости МТ для каждого значения m и t построим перпендикуляр с высотой, определяемой этой функцией, то получим плоскость Q, показанную на Рис. 1.
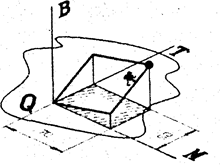
Рис.1
Оптимальна точка должна находиться в этой плоскости. Но плоскость не имеет границ, и оптимальное решение найти нельзя. Вспомним о реальных возможностях магазина (70 магнитофонов м 50 телевизоров) и добавим, что количество проданных телевизоров и магнитофонов не может быть отрицательным. Этими 4-мя условиями (неравенствами) и определяются ограничения, которые в плоскости МТ образуют заштрихованный прямоугольник. Значит, оптимальная выручка на приведенном рисунке определяется точкой на плоскости Q над этим прямоугольником. Теперь достаточно "пройти" по точкам вдоль проекции прямоугольника на плоскость, которая показана на рисунке жирной линией, и найти самую высокую точку. Она и будет оптимальной.
Рассмотренный пример относится к области линейного программирования. Большое количество экономических задач сводятся к линейному программированию. Задачи линейного программирования можно решать разными методами, например графическим или симплекс-методом, а можно использовать прикладные программы.
Далее на примерах рассматривается использование для этой цели табличного процессора Ехсеl, вместе с его инструментальным средством Solver (Решатель). Первые 4 примера рассмотрены детально. Приводится подробная информация о средствах интерфейса и параметрах. Остальные 3 примера следует решить самостоятельно.
Планирование производства.
Рассмотрим для начала простую задачу планирования производства. Предположим, что небольшая фабрика выпускает два вида красок: А и Б. Продукция поступает в оптовую продажу. Для производства используется два вида исходных продуктов: В и Г. Максимально возможные суточные запасы этих продуктов составляют 6т и 8т соответственно. Расходы продуктов на 1 т красок приведены в Таблице. I.
Таблица 1.
| Исходный продукт | Расход на 1т краски | Максимальный запас | |
| Краска А | КрасквБ | ||
| В Г |
Анализ рынка показал, что суточный спрос на краску А не превышает спроса на краску Б более чем на 1т. Кроме того установлено, что спрос на А не превышает 2т в сутки. Прибыль от продажи красок А и Б равны 3 ОООр и 2 ОООр соответственно.
Необходимо найти количество выпускаемых красок, при котором прибыль максимальна.
Для решения задачи необходимо построить математическую модель, Дяя этого необходимо получать ответы на три вопроса:
1) для определения каких величия строится модель (переменные) ?
2) что оптимизируется (функция цели)?
3) при каких условия определяется решение (ограничения) ?
В нашем случае необходимо так спланировать объем производства красок, чтобы максимизировать прибыль. Поэтому переменными являются суточный объем производства красок ХА и ХБ.
Суммарная суточная прибыль от производства составляет:
П=3000*ХА+2000*ХБ
Перейдем к ограничениям. Объем производства не может быть отрицательным, следовательно
ХА,ХБ>=0.
Расход исходного продукта не может превосходить максимального запаса, следовательно
ХА+2*ХБ<=6,
2*ХА+ХБ<=8
Ограничение на спрос таковы, что должны выполняться неравенства
ХА-ХБ<=1,
ХБ<=2.
Математически задача формулируется следующим образом.
Необходимо максимизировать функцию
П=3000*XА+2000*XБ
При ограничениях
ХА+2*ХБ<=6,
2*ХА+ХБ<=8,
ХА-ХБ<=1,
ХБ<=2,
ХА, ХБ>=0.
Решим поставленную задачу с помощью команд: Сервис, Поиск решения. Если в меню Сервисотсутствует команда Поиск решения, то необходимо выполнить последовательно: Сервис, Надстройка, Поиск решения.
Решение задачи начинаем с подготовки данных. Введем необходимые данные и ограничения следующим образом (Рис2)

Рис.2
Выберем команды: Сервис, поиск решения. Заполним окно диалога Поиск решения (Рис3).
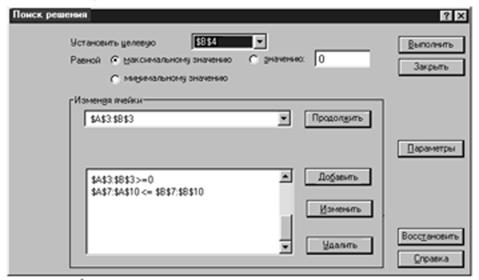
Рис.3.
При этом параметры поиска в окне Параметры поиска решения
установлены следующим образом (Рис4).
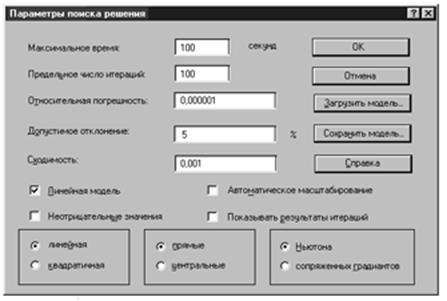
Рис.4.
После команды Выполнить откроется окно диалога Результаты поиска решения, которое сообщает, что решение найдено (Рис5)
 Рис.5.
Рис.5.
Оптимальный план производства и соответствующая прибыль появятся в исходной таблице. Из нее следует, что оптимальным является производство 3,333т краски А и 1,333т краски Б. Этот объем производства обеспечивает максимальную прибыль 12666,7 (Рис7).
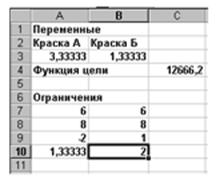 Рис.7.
Рис.7.
Для того чтобы вывести отчет о результатах решения, в окне Результаты поиска необходимо указать требуемый тип отчета: Результаты, Устойчивость, Пределы. Затем в рабочей книге выбрать появившийся корешок (Рис8)
Компьютерные сети
Основные понятия и определения
Реализация современных информационных систем немыслима без компьютерных сетей.
Компьютерная сеть – это совместное подключение нескольких отдельных компьютеров к единому каналу передачи данных. Основное назначение компьютерной сети состоит в совместном использовании информационных ресурсов и осуществление быстрой связи как внутри организации, так и за ее пределами.
Рассмотрим основные понятия, используемые в компьютерных сетях:
1. Клиент сети – это элемент сети, который потребляет информацию или является ее источником. Примером типичного клиента является рабочая станция. Рабочая станция представляет собой обычный персональный компьютер, работающий под управлением собственной операционной системы. Однако в отличие от автономного персонального компьютера рабочая станция содержит плату сетевого адаптера, соединена с сервером и использует операционную систему, которая позволяет обмениваться информацией с другими клиентами сети.
2. Сервер (server) – компьютер, предоставляющий свои ресурсы клиентам сети.
Любой компьютер, работающий в сети, может выполнять функции, как клиента, так и сервера, либо совмещать обе эти функции. Если выполнение каких-либо серверных функций является основным назначением компьютера (например, предоставление файлов в общее пользование или организация совместного использования принтера, или предоставление всем пользователям сети возможности запуска на данном компьютере своих приложений), то такой компьютер называется выделенным сервером. В зависимости от выполняемых функций различают следующие типы серверов:
· файловый сервер предназначен для хранения и предоставления файлов, с которыми работают пользователи;
· сервер баз данных обеспечивает доступ клиентам к общим базам данных;
· сервер приложений служит для предоставления пользователям компьютерных программ;
· сервер печати обеспечивает печать на общем печатном устройстве со всех рабочих мест;
· Web-сервер обеспечивает предоставление информации через сеть Internet;
· почтовый сервер (сервер E-mail) обеспечивает циркуляцию электронной почты, как внутри организации, так и во внешней сети.
3. Среда – способ соединения компьютеров в сети. В качестве среды может выступать электрический кабель, инфракрасная связь, радиосвязь и т.д.
4. Ресурсы сети – это различные элементы, используемые в сети. Компьютеры, входящие в компьютерную сеть, могут использовать следующие ресурсы:
· данные (т.е. файлы);
· принтеры;
· модемы и факс-модемы;
· винчестеры и флоппи-дисководы;
· дисководы CD-ROM, DVD и т.д.
5. Трафик сети – объем передаваемых сообщений за некоторый интервал времени.
В зависимости от размера все компьютерные сети делятся на:
1. Локальные вычислительные сети (ЛВС), абоненты которых сосредоточены на расстоянии не более 10 - 15 км (или в пределах одного здания). К ЛВС относятся вычислительные сети отдельных предприятий, банков, фирм, офисов и т.д.
2. Региональные вычислительные сети (районные, городские, областные), абоненты которых сосредоточены на расстоянии от десяти до несколько сотен километров. Региональные сети могут включать абонентов внутри города, области, республики.
3. Глобальные вычислительные сети, абоненты которых сосредоточены на расстоянии 1000 и более километров. Глобальные сети позволяют решить проблему объединения информационных ресурсов целых стран и даже всего человечества. Наиболее известны следующие глобальные сети: Internet, Fido, Sprint, Relcom и т.д.
Использование компьютерной сети в любой организации дает следующие преимущества, которые приведены ниже.
Разделение ресурсов – позволяет экономно использовать ресурсы в информационной системе. Например, производить печать со всех компьютеров на одном принтере, использовать один дисковод DVD и т.д.
Разделение данных – позволяет иметь доступ с разных рабочих мест к базам данных, расположенных на других компьютерах. Благодаря разделению данных можно организовать работу нескольких пользователей по созданию общего документа.
Разделение программных средств – позволяет пользователем использовать программы, установленные на других компьютерах.
Использование электронной почты – компьютерная сеть позволяет оперативно рассылать служебные записки, доклады и сообщения всем сотрудникам организации.
Дата добавления: 2015-11-18; просмотров: 2912;
