Приложение. Законы динамики вращательного и поступательного движений.

Рассмотрим блок радиуса R с моментом инерции J, который может вращаться вокруг горизонтальной оси (рисунок 2).

Через блок перекинута невесомая, нерастяжимая нить, на концах которой висят грузы массой m каждый. Если на один из грузов (на рисунке – на правый) положить перегрузок достаточно большой массы ∆m, система придёт в движение (разумеется, при отсутствии сил трения перегрузок сколь угодно малой массы приводит систему в движение, но при наличии сил трения это не так). Найдём ускорения грузов, считая, что при движении нить по блоку не сколь­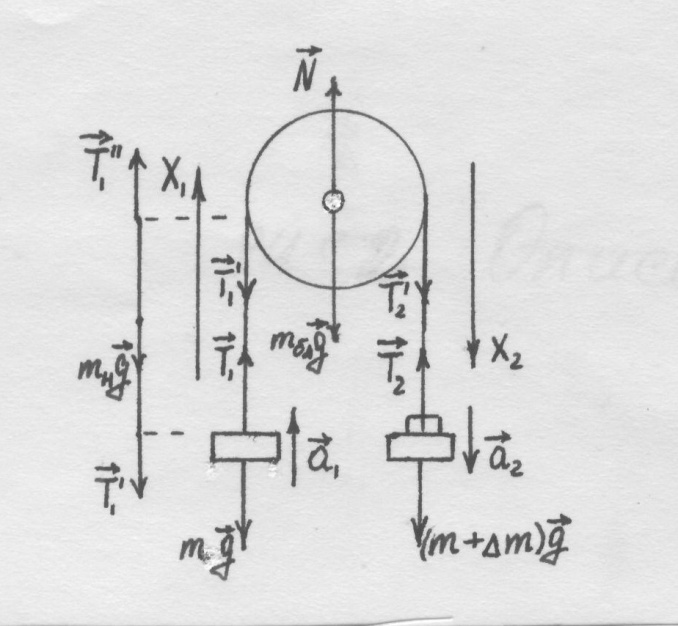 зит. Будем считать, что диссипативные силы, за­висящие от скорости (например, силы сопротивления воздуха) отсутствуют. На левый груз действует сила тяжести 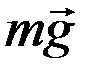и сила 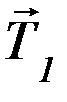со стороны нити. На левый вертикальный участок нити действуют две силы: сила 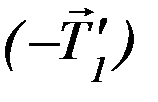со сторо­ны левого груза, которая по III закону Ньютона равна силе 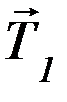по модулю и противоположна по направлению, и сила 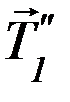со стороны участка нити, находящегося на блоке. На рисунке слева отдельно показан левый участок нити и силы, на него действующие; напомним, что нить считается невесомой. Запишем второй закон Ньютона для левого участка нити:

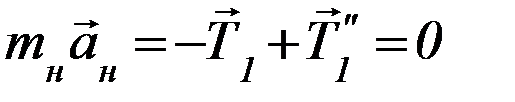, поскольку m_нити = 0

Тогда, 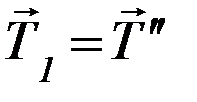. По третьему закону Ньютона сила 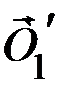, с которой левый вертикальный участок нити действует на участок, находящийся на блоке, равна

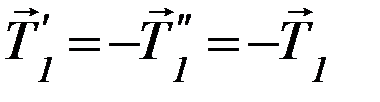
Фактически, сила 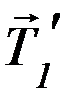оказывается приложенной к блоку, поскольку в отсутствие проскальзывания блок и участок нити, находящийся на нём, составляют единое целое.

Аналогичные рассуждения применимы и для правого вертикального участка нити. Для модулей сил, следовательно, имеем

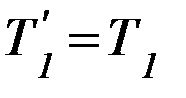и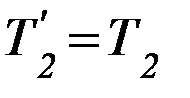

Запишем систему уравнений, описывающих поступательное движение обоих грузов. Для этого выберем положительное направление осей Х₁ и Х₂ так, чтобы они совпадали с направлением движения тел (такой выбор осей называется согласованным).

Тогда для висящих грузов, которые движутся поступательно, второй закон Ньютона при движении тел на первом этапе (S₁):

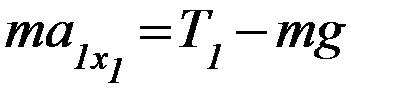(П-1)

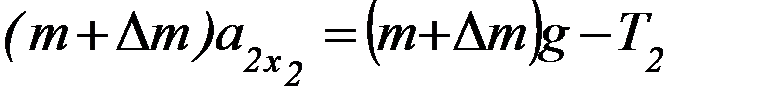(П-2)

Вследствие нерастяжимости нити модули перемещений грузов на обоих концах нити одинаковы. Одинаковы модули скоростей и ускорений грузов, но направления их, конечно, противоположны:

,

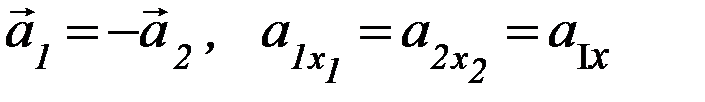где а – модуль ускорения каждого груза.

При этом 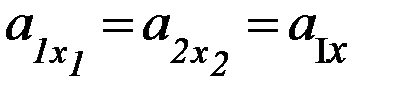ускорения грузов на этапе I.

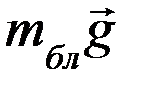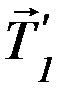Рассмотрим теперь силы, которые действуют на блок. Помимо силы тяжести , сил и 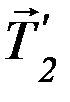, о которых шла речь выше, на блок действует сила реакции оси 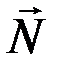, а также силы трения в оси блока. Детальный анализ сил трения очень сложен, поэтому ограничимся рассмотрением упрощённой модели, которая достаточно хорошо подтверждается опытом. Для вращения блока существенны не сами силы трения, а их моменты относительно оси вращения. Поскольку центр масс блока покоится, то 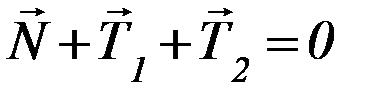. Переходя к модулям сил, получим:

.

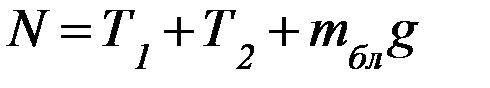Запишем для блока основное уравнение динамики вращательного движения

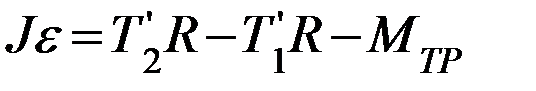(П-3)

Если блок невесом, то J_бл. = 0 и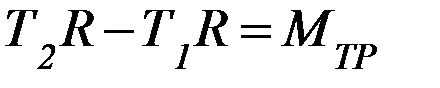

Если нить по блоку не скользит, то модуль скорости грузов равен модулю линейной скорости точек на окружности блока:

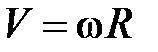
Дифференцируя это соотношение по времени, получим следующую связь модуля ускорений грузов а и углового ускорения ε:

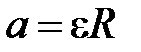
Тогда (П-3) можно переписать в виде

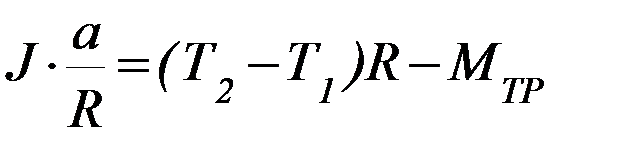(П-4)

Решая систему уравнений (П-1), (П-2), (П-4), получим выражение для модуля ускорений грузов при движении и на первом этапе

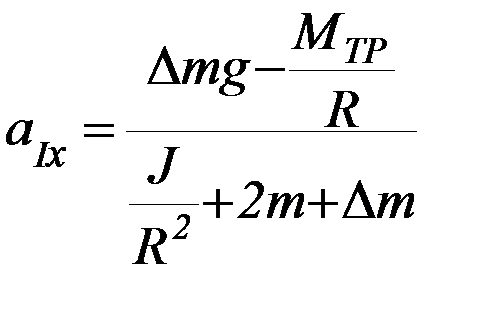(П-5)

Если блок невесом: 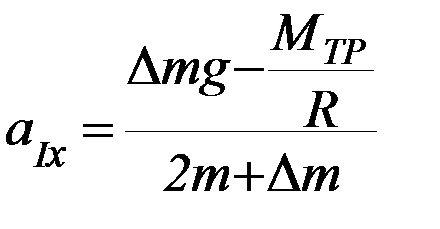(П-6)

Если система некоторое время движется с ускорением а_Iх на этапе 1, а затем перегрузок снимается, то дальнейшее движение системы на этапе 2 будет происходить с ускорением а_IIх, выражение для которого вытекает из формулы (П-6) при ∆m = 0:

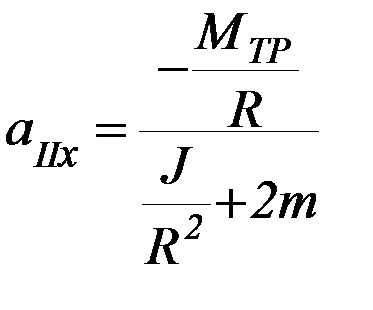(П-7)

Если блок невесом: 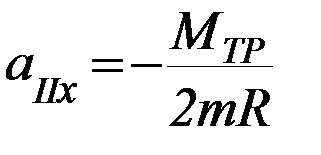(П-8)

Знак «минус» показывает, что движение вследствие наличия сил трения будет замедленным.

Аналогичное выражение для ускорения а_IIx можно получить, если записать законы поступательного и вращательного движения на этапе 2 в отсутствие перегрузка и невесомости блока:

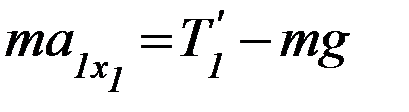(П-9)

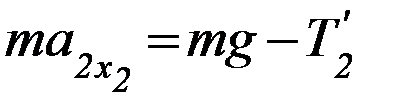(П-10)

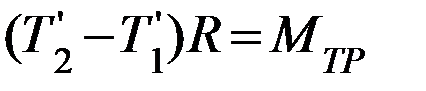(П-11)

где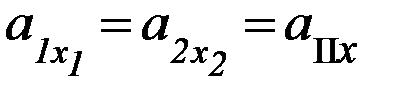

В работе правый груз проходит с перегрузком задаваемый экспериментатором путь S₁ (этап 1)_, а затем перегрузок снимается и измеряется время движения на пути S₂, который тоже задаётся экспериментатором (этап 2). Поскольку во всех случаях ускорения а_Iх и а_IIx – постоянные величины, справедливы все известные из школьного курса физики формулы кинематики.

В частности, поскольку движение с перегрузком начинается без начальной скорости, скорость правого груза в конце этапа 1 (она же является начальной скоростью на этапе 2) связана с путём S₁ соотношением:

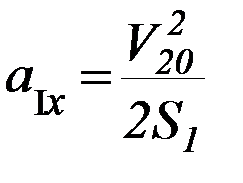(П-12)

Время движения t на этапе 2 связано с выражением для пути S₂ формулой:

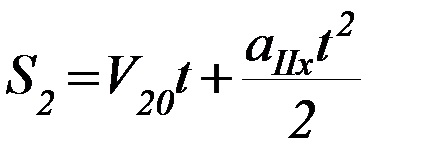(П-13)

Если массой блока можно пренебречь, то при подстановке формул (П-6), (П-8), (П-12) в (П-13) получим следующее выражение для определения момента сил трения:

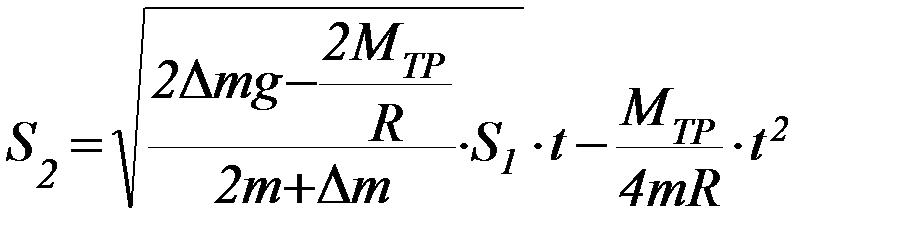(П-14)