Шектелмеген жағдайларда жасалынатын әрекеттер

Жоғарғы тақырыпта қарастырылып отырған есептердің шешімі әрқашан да бірден табыла бермейтінін атап өттік. Мұндай жағдай көбінесе қорларды өндірілетін өнім бойынша бөлгенде, есептің шарты жүйеде бірікпеген немесе мақсат функция шектел-меген жағдайларда пайда болады. Бірінші кезекте жүйеде шектеулердің сәйкестендірілмеген жағдайында қандай әрекеттер жасау керектігін қарастырайық. Есепте, оңтайлы шешім бойынша шаруашылыққа 1-ші (х₁ = 250 ө.б.) және 3-ші (х₃ = 535,71 ө.б.) өнімдерді өндірумен айналысу пайдалы делінді. Осы жағдайда еңбек шығыны және қаржы толығымен қолданылатынын байқадық (1.9-сурет). Жүйеде шектеулердің сәйкестендірілмеген жағдайын жасанды тудыру үшін, оңтайлау шешімін сақтап, бірақ 2-ші өнімді 100 ө.б. кем емес өндіру керек делік. Бұл жалған шарт, оқу мақсаты үшін қарастырылып отыр. Сөзсіз, ол қорлардың жетіспейтіндігіне әкеледі де, шектеулер бірікпеген деп Поиск решения хабарлайды (1.10-сурет).

Excel-де мұндай шектеулердің бірікпеген жағдайынан қалай өтуге болатынын қарастырайық. Ол үшін есептің математикалық моделіне көңіл аударайық. Шектеулердің бірікпеген себебін білу үшін керекті қосымша қорды u_i модельге енгізейік, яғни модельді мына түрде жазамыз:

Z= 135х₁+125х₂ + 150х₃ +130х₄ → max

мына жағдайда:

1,9х₁+ 1,77х₂ + 2,1х₃ + 2 х₄ = 1600 + u₁

9,5х₁+ 8х₂ + 10,5х₃ + 8,9х₄ = 9000 + u₂

10х₁+ 7,5х₂ + 14х₃ + 7,3 х₄ = 10000 + u₃

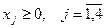; u_i ≥ 0, i =1,2,3.

Есепті осылай қою, керекті қосымша қорлардың u₁, u₂, u₃ минимальды мәнін анықтауға мүмкіндік береді. Сондықтан беріл-ген жүйені мына түрде жазайық:

F= u₁+ u₂ + u₃ → min

Z= 135х₁+125х₂ + 150х₃ +130х₄

1,9х₁+ 1,77х₂ + 2,1х₃ + 2 х₄ – u₁= 1600

9,5х₁+ 8х₂ + 10,5х₃ + 8,9х₄ – u₂ = 9000

10х₁+ 7,5х₂ + 14х₃ + 7,3 х₄ – u₃ = 10000

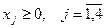; u_i ≥ 0, i =1,2,3.

Осыдан кейін 1.3-суреттегі кестелік модельге біраз өзгерістер енгіземіз. Енгізілген өзгерістер 1.13-суретте көрсетілген. Бірінші-ден, жаңа айнымалылар белгілері F3:H3 аралығындағы бағаналарға жазылғанда, ал олардың мәндері үшін F4:H4 аралығын тағайын-далған. Екіншіден, шектеулерге осы жаңа айнымалылардың (u₁, u₂, u₃) бағаналарына олардың коэффициентері (-1) жазылады.

Жаңа мақсат функция үшін 5-ші жолда жаңа айнымалы-лардың (u₁, u₂, u₃) бағаналарына олардың коэффициенттері (1) жазылады да, ал I5-ұяда оның мәні анықталынады. Ескі мақсат функция формуласы өзгеріссіз қалады (1.13-сурет).

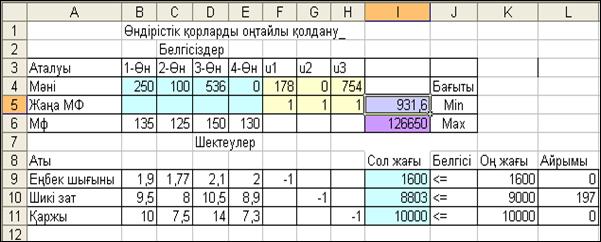
1.13-сурет

Сервис.. Поиск решения..Мақсат функцияны (I5-ұя) мини-мальды мәнін іздеуге орналастырамыз. Изменяя ячейки терезесіне B4:H4. Осыдан кейін шектеулердің шарттарын енгіземіз: B4 =250; C4 = 100; D4 = 536 және E4:H4>=0. Есеп Выполнить бұйрығы бойынша шешуге жіберіледі. Есептің шешімі 1.13-суретте берілген. Суреттен көріп отырмыз ізделініп отырған қосымша қорлардың мөлшері u₁ = 178ө.б. , u₃ = 754 ө.б. және u₂ = 0. Сөйтіп, өнімдер-ді берілген көлемде өндіру үшін шаруашылықтағы қорлар мөлшері болу керек:

еңбек қоры 1600 + 178 = 1778 ө.б.;

шикізат 9000 + 0 = 9000 ө.б.;

қаржы 10000 + 754 = 10754 ө.б.

Осы жағдайда 126650 а.б. пайда алынады.

Шектеулер жүйесінде теңсіздіктер сәйкестендірілмеген жағ-дайда мұндай әдісті қолдану өте құнды. Егер нақтылы шаруа-шылықтың жағдайында көрсетілген деңгейге дейін қорларды көбейтуге мүмкіндік жоқ болса, онда алғашқы есептің қойылуы сияқты, ізделініп отырған айнымалыларға теріс болмау шартын жазамыз да (х_i≥0), есепті қайта шығарамыз. Онда шаруашылықтағы қорлардың мүмкіндіктеріне сәйкес жаңа шешім алынады. Сөзсіз, пайда азайады.

Мақсат функцияның шектелмеуі туралы Поиск решения-дан мынадай хабарлама алынады: Значения целевой ячейки не сходятся.

Мақсат функцияның шектелмеуі екі жағдайда байқалады. Мақсат функцияның шексіз үлкеюуіне немесе кемуіне жібермейтін есептің шешімдері мүмкін бола алатын аймақ шектелмеген болса, онда есеп шешілмейді. Сондықтан:

· мақсат функция максимумге ізделінсе есептің шешімдері мүмкін бола алатын аймақ жоғарыдан шектелуге тиіс;

· мақсат функция минимумге ізделінсе есептің шешімдері мүмкін бола алатын аймақ төменнен шектелуге тиіс.

Осы ережелерді ұққаннан кейін, мақсат функцияның шектел-меуін жеңіл түзетуге болады. Есептің шартын және шектеу белгі-лерін тексеріп, мүмкіндігінше түзетулер енгізіледі. Қосымша шектеу енгізу мүмкіндіктері қарастырылады.