Многократных измерений

При многократных измерениях погрешность измерения от случайных ошибок уменьшается в 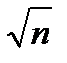раз, где 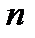- число измерений.

На основе закона нормального распределения случайных величин можно многократным измерением одних и тех же величин одним и тем же измерительным средством уменьшить влияние случайных ошибок, так как они усредняются и, в итоге, повышается точность результата измерения.

Проведя несколько повторных измерений одной и той же величины и получив различные результаты, определяют среднее арифметическое значение ряда измерений 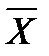и принимают его за значение измеряемой величины 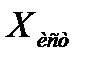, т. е. принимают

.

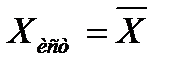Ценность результата многократных измерений значительно повышается, если кроме среднего арифметического значения 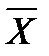будет определена предельная погрешность среднего арифметического в виде S, которая зависит от значения и количества проведения измерений .

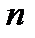Предельная погрешность среднего арифметического S определяется по формуле

,

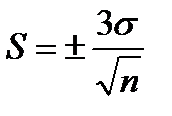где – средняя квадратическая погрешность ряда измерений.

Следовательно, при ответственных измерениях проводят ряд повторных измерений (5—10) и на основе полученных результатов всех измерений подсчитывают среднее арифметическое значение и среднюю квадратическую погрешность , а потом и предельную погрешность среднего арифметического S. После этого истинное значение измеряемой величины 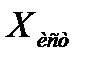представляется так:

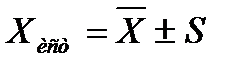или .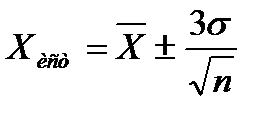

В случае многократных повторных измерений одной и той же величины одним и тем же методом измерения и при отсутствии систематических погрешностей за предельную погрешность метода измерения, обозначаемую 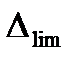принимается значение, равное .

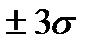Если при многократных измерениях появится погрешность больше 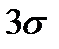, то такую погрешность считают грубой погрешностью, и результат измерения с такой погрешностью отбрасывают. Причинами грубой погрешности могут быть неправильное снятие показаний по шкале прибора или описка при записи результата измерения и другие грубые ошибки.