Понятия о погрешностях измерений, видах и источниках их

Узнать абсолютное значение измеряемой величины нельзя, так как результаты наших измерений не свободны от погрешностей. Поэтому измерения одной и той же постоянной величины при сохранении одних и тех же внешних условий часто дают неодинаковые результаты, отличающиеся на небольшую величину. Погрешностью измерения 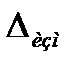называется отклонение результата измерения 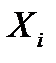от истинного значения :

.

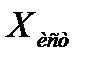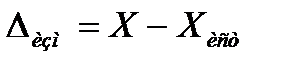Погрешности измерений подразделяют на систематические, случайные и грубые (промахи).

Систематические погрешности. Систематической называется такая погрешность, значение которой при повторных измерениях повторяется или закономерно изменяется. Эти погрешности либо увеличивают результат каждого измерения, либо уменьшают его на одну и ту же величину. Например, если измерительную, головку установить на нуль по концевой мере, действительный размер которой меньше номинального на 1 мкм, то при всех измерениях будет погрешность 1 мкм со знаком минус.

Влияние систематических погрешностей можно устранить, если ликвидировать причины их появления или внести поправку в результат измерений, равный величине погрешности, но с обратным знаком, как, например, это делается, когда известно, что часы уходят вперед на 3 мин.

Случайные погрешности. Случайной называется погрешность измерения, принимающая при повторных измерениях одной и той же величины и в тех же условиях разные значения по величине и знаку.

Случайные погрешности вызываются многочисленными случайными причинами: влиянием неодинаковости измерительного усилия, влиянием зазора между деталями измерительного прибора, погрешностью при отсчете показаний прибора, неточностью установки измеряемого изделия относительно измерительного устройства и др.

Величину и знак возможной случайной погрешности заранее, т. е. до проведения измерения, установить нельзя. Практикой установлено, что распределение случайных погрешностей измерений в большинстве случаев близко к закону нормального распределения. Поэтому допускают, что погрешности, одинаковые по величине, но разные по знаку («+» и «—»), равновероятны. Наибольшее число измерений имеют малые погрешности, близкие к нулю (малые по величине погрешности встречаются чаще, чем большие). Ввиду того что одинаково вероятны как плюсовые, так и минусовые случайные погрешности, при достаточно большом количестве повторных измерений среднее арифметическое значение ряда повторных измерений дает наиболее точное значение измеряемой величины (размера).