Число 1.02·10-8 см2 принимается за 1 дарси (Д).

Дифференциальные уравнения фильтрации подземных вод

Закономерности движения подземных вод описываются дифференциальными уравнениями. Они позволяют сделать количественную оценку параметров движения при решении конкретных гидрогеологических задач. Для получения основных дифференциальных уравнений фильтрации и их решения необходимо знание следующих уравнений, описывающих условия движения подземных вод:

· Уравнения движения (определяет закон фильтрации);

· Уравнение состояния жидкости в пористой среде (закон сохранения энергии);

· Уравнения неразрывности потока (закон сохранения массы).

Для визуального пояснения дальнейших переменных и их символов ниже изображена условно область фильтрации и ее разбивка на элементарные участки (элементарные объемы), состоящие из слоев (Layers), столбцов (Columns) и рядов (Rows).

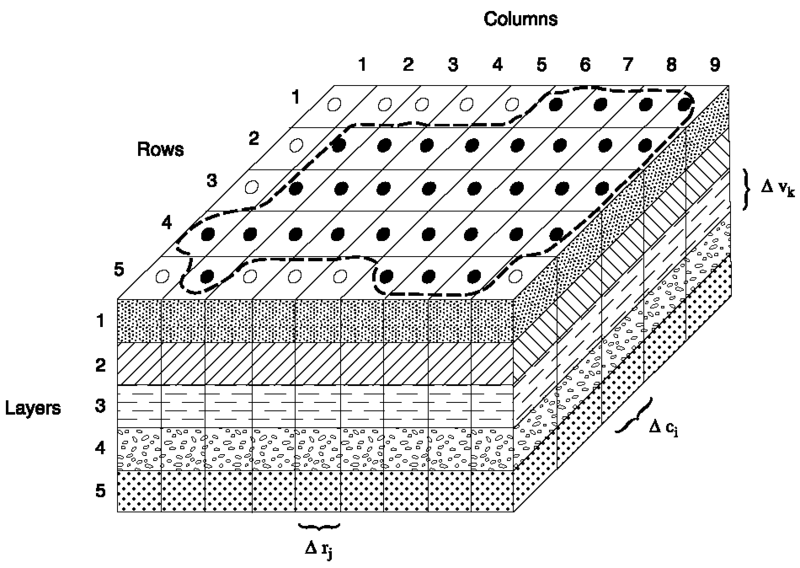
Рисунок – Разбиение гидрогеологической системы на элементы.

Уравнение движения подземных вод. Из линейного уравнения движения Эйлера для идеальной жидкости пренебрегая силами инерции можно получить уравнения для компонент скорости:

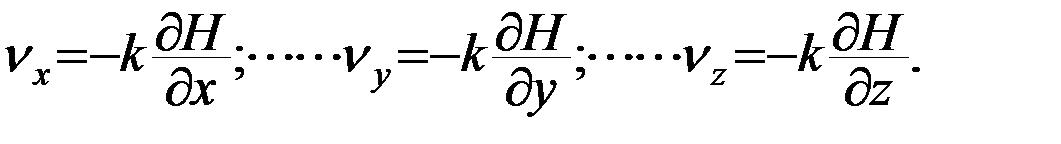( 19 )

Эта система представляет собой закон Дарси, выраженный в дифференциальной форме в частных производных. В общем виде это можно записать через вектор скорости :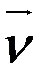

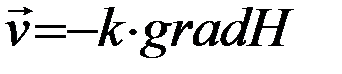( 20 )

uде grad H – вектор градиента пьезометрического напора H. Учитывая связь между . . коэффициентами фильтрации k и проницаемости k_П ( 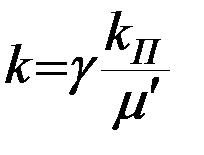) , а также между давлением Р и напором Н ( 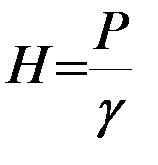), выражение ( 19 ) принимает вид, используемый в нефтяной гидрогеологии:

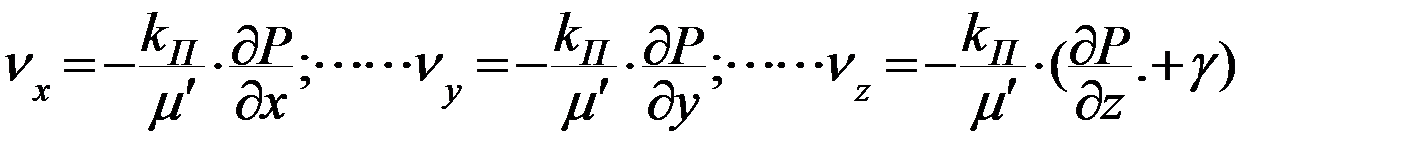(21)

Уравнение состояния. В практике плотность жидкости γ и динамический коэффициент вязкости µ' – зависят от давления и температуры, тогда состояние жидкости запишем в виде

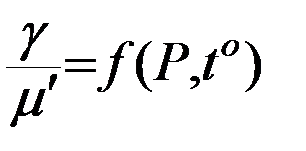( 22 )

С учетом возможного изменения объема порового пространства (и активной пористости n_а при изменении давления, уравнение состояния пористой среды примет вид:

n_а = f(P) ( 23 )

Будем считать, что подземная вода и пористая среда несжимаемы и изотропны. Плотность воды γ постоянна и активная пористость – неизменна, т.е.

γ = const. ( 24 )

n_а = const. ( 25 )

При этом разность пьезометрического напора становится основной действующей силой несжимаемой жидкости в несжимаемой пористой среде. Режим фильтрации при таких условиях называют водонапорным (либо жестким водонапорным).

Уравнение неразрывности потока. Подземный поток воды движется без образования в нем пустот и разрыва сплошности. При этом он подчиняется уравнению неразрывности, который отражает закон сохранения массы движущейся воды.

Для жесткого режима фильтрации уравнение неразрывности имеет вид:

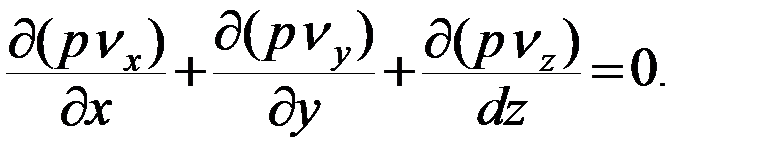( 26 )

Для установившейся фильтрации в плоскости xy уравнение упрощается:

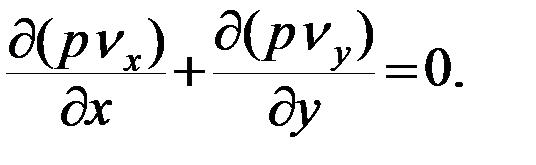( 27 )

Основные уравнения фильтрации подземных вод. Получение основных дифференциальных уравнений фильтрации подземных вод производят двумя методами:

• (1) Метод синтеза трех рассмотренных видов уравнений – уравнения движения подземных вод, (2) уравнения неразрывности потока и (3) уравнения состояния жидкости и пористой среды;
• Балансовым методом, который рассматривает изменение баланса элементов потока подземных вод.

Так, например, при жестком режиме фильтрации уравнения движения потока воды при соблюдении линейного закона Дарси имеют вид:

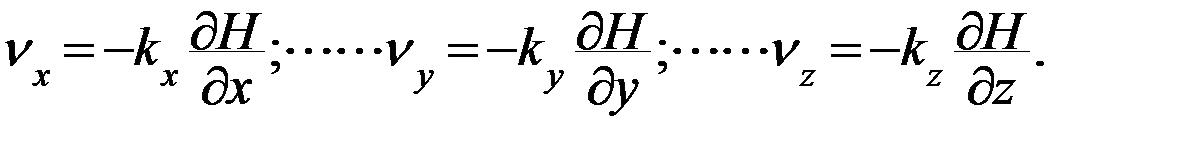( 28 )

При этом жидкость и пористая среда несжимаемы

γ = const, n = const. ( 29 )

Уравнение неразрывности при этом запишется в виде:

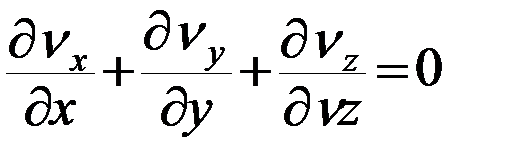( 30 )

Подставив сюда компоненты скорости из (28) имеем дифференциальное уравнение фильтрации:

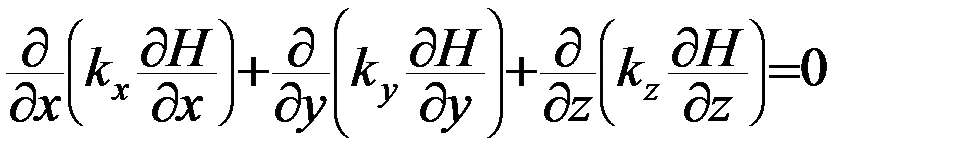. ( 31 )

Это простейшее уравнение носит название уравнение Лапласа.

Основные гидродинамические элементы потока. Под потоками подземных вод принято понимать пространственно оконтуриваемые потоки, движение которых происходит в пористой или трещиноватой среде под действием градиента гидростатического напора или давления. Основные элементы такого потока – его мощность, ширина, величина напора, гидравлический уклон, скорость фильтрации, расход, линии токов, линии равных напоров.

Мощность потока водонасыщенных пород h, m;

Ширина потока в сечении перпендикулярном направлению его движения В;

Напор потока – величина пьезометрического напора Н. Для малых скоростей фильтрации скоростным напором ν²/2g можно пренебречь, Н определяется сумой первых двух членов уравнения Бернулли (пьезометрической высоты 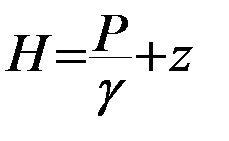и высотой положения над плоскостью сравнения z), т.е. Н = z + Р/γ ( получено из уравнения (3) --Н + ν²/2g = const)

Скорость фильтрации ν- это расход потока отнесенный к площади поперечного сечения (величина фиктивная). Действительное движение воды в порах среды ν_Д будет всегда выше.

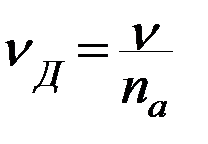( 32 )

Здесь n_a - активная пористость фильтрационной среды.

Расход потока при линейном законе фильтрации определяется из скорости фильтрации ν и площади сечения потока F. Т.е. полный расход Q = ν·F. Обычно определяют единичный расход q.

Для грунтового потока q = Q / B_cp = k _cp·I _cp·h _cp ( 33 )

Для напорного потока q = Q / B_cp = k _cp·I _cp·m _cp ( 33 )

В дифференциальной форме:

Для грунтового потока 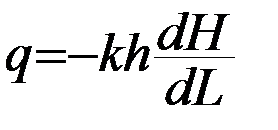( 34 )

Для напорного потока 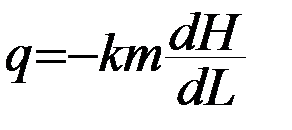( 35 )

Линии токов определяют направление движения потока и совпадают с направлением движения частиц жидкости. Типичным примером сходящегося радиального потока является движение воды к эксплуатационной скважине.

Расход радиального потока выражается формулой Дюпюи:

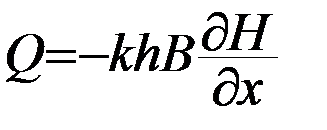( 36 )

С учетом же линейного изменения ширины потока В она имеет вид:

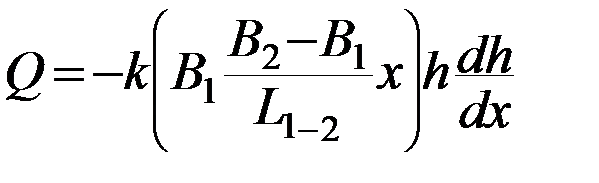( 37 )

После интегрирования последнего уравнения для общего расхода грунтового радиального потока при горизонтальном залегании водоупора получаем:

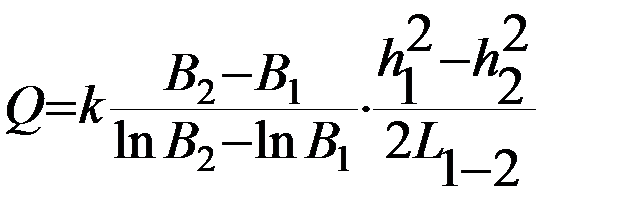( 38 )