Линейный закон фильтрации

Линейный закон фильтрации применим к ламинарному движению воды и был установлен экспериментально в 1856 г. Французским гидравликом Ф. Дарси. Проведенный им опыт поясняется на следующем рисунке:

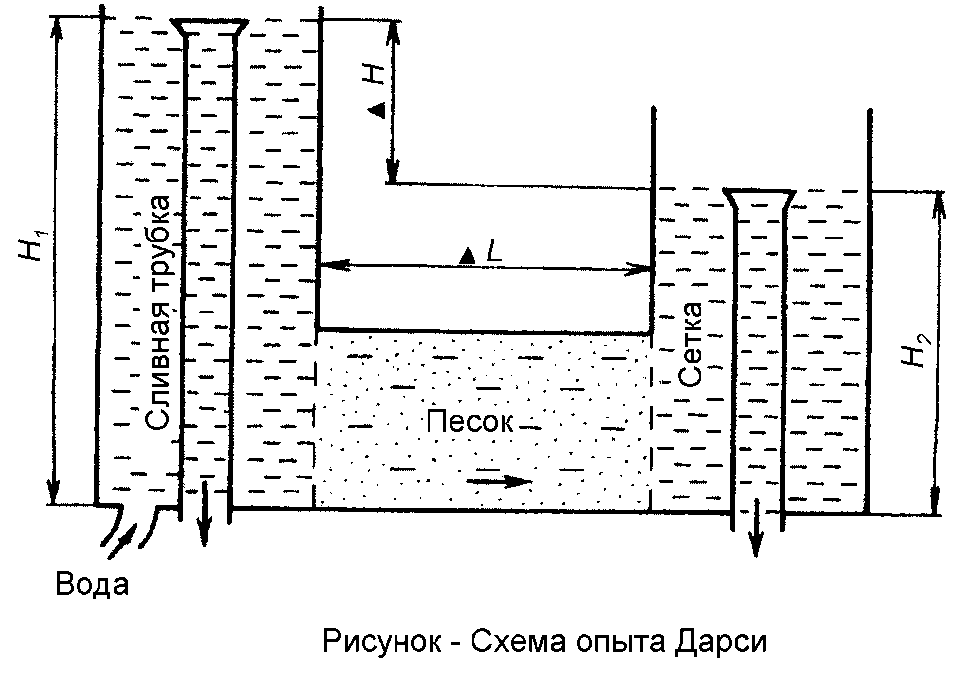
В заполненную песком трубку слева подается вода, проходя фильтруясь через песок она сливается через вторую трубку справа. При этом поддерживаются постоянные уровни Н₁ и Н₂. Определяли расход воды в зависимости от разности уровней ΔН = Н₁ и Н₂, длины фильтра ΔL и его площади поперечного сечения F.

Было установлено, что количество воды Q прямо пропорционально Fи ΔН и обратно пропорционально длине пути фильтрации ΔL:

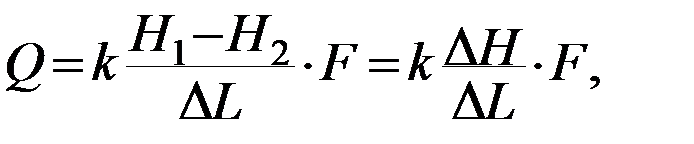( 5 )

Где коэффициент k принято называть коэффициентом фильтрации.

Член 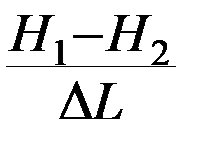= 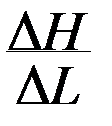показывает как изменяется уровень вдоль пути фильтрации и называется напорным или гидравлическим градиентом (уклоном). Его часто обозначают как I. Если разделить обе части ( 5 ) на площадь F и с учетом того, что скорость фильтрации 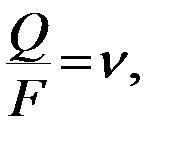получим для закона Дарси выражение:

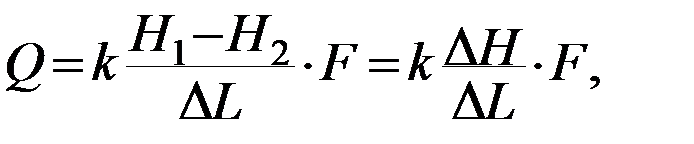(6)

Оно представляет собой линейную зависимость скорости фильтрации от гидравлического градиента. Здесь скорость пропорциональна напорному градиенту. В дифференциальной форме линейный закон фильтрации описывается уравнением:

ν=-k 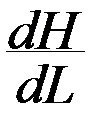, ( 7 )

Минус показывает что скорость течения увеличивается в сторону обратную увеличению напора Н.

Нарушение линейного закона Дарси имеет место при больших скоростях фильтрации, для неньютоновских жидкостей, иногда и для очень малых скоростей. Верхний предел его применимости связан с понятием критической скорости фильтрации. Этот термин введен Павловским Н.Н. и связан с понятием числа Рейнольдса Re, используемого чтобы разграничить ламинарный и турбулентный вид движения воды.

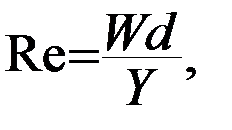( 8 )

где W – средняя скорость движения воды (см/с), d – диаметр трубки с водой (см), а

Y = µ΄/ γ – называют кинематическим коэффициентом вязкости (см²/с), µ΄ - динамический коэффициент вязкости (пуазы – пз), γ – плотность воды (г/см³).

Н.Н. Павловский изменил уравнение ( 8 ) введя в него вместо диаметра трубки d и средней скорости движения воды W действующий диаметр зерен d_е пористость n и скорость фильтрации ν и получил уравнение:

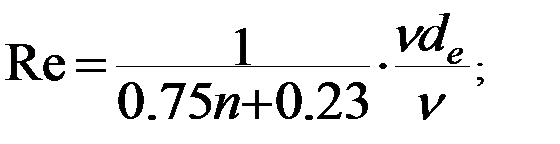( 9 )

Было выявлено, что отклонение от линейного закона Дарси происходят при критических значениях Re = 7/5 – 9. Соответствующая им скорость ν_кр названа критической. Исследованиями показано, что при скоростях воды менее 1000 м/сут применим линейный закон Дарси. При скоростях выше 1000 м/сут используют нелинейный закон Дарси, установленный А.А. Краснопольским:

ν = 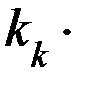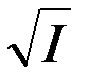( 10 )

где k_к - коэффициент фильтрации Краснопольского. Его формула имеет вид:

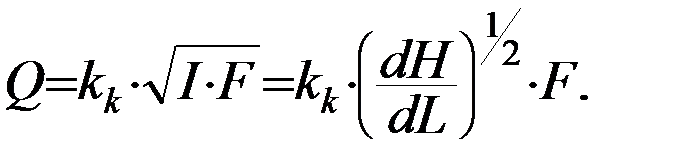( 11 )

Отсюда следует, что для турбулентного движения скорость потока Q пропорциональна гидравлическому градиенту в степени ½. А связь напорного градиента I со скоростью ν записывают и в виде квадратичной зависимости:

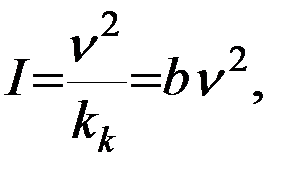где b – коэффициент пропорциональности ( 12 )