Частные случаи определения риска портфеля инвестиций при разных значениях коэффициента корреляции
· Если 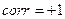 ,то формула определения риска для портфеля, состоящего из двух активов, будет иметь следующий вид:
,то формула определения риска для портфеля, состоящего из двух активов, будет иметь следующий вид:
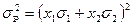 это дисперсия
это дисперсия
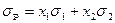 это риск портфеля
это риск портфеля
|
|
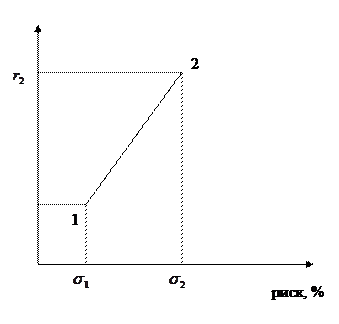
Рис. 1 График зависимости доходности портфеля от го риска при коэффициенте корреляции = +1.
На линии 1-2 отражены все возможные портфели, которые мы можем составить из 2-ух активов с коэффициентом корреляции = +1.
· Если 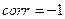 , то формула определения риска для портфеля, состоящего из двух активов, будет иметь следующий вид:
, то формула определения риска для портфеля, состоящего из двух активов, будет иметь следующий вид:
 это дисперсия
это дисперсия
 - это риск портфеля
- это риск портфеля
График зависимости доходности портфеля от его риска представлен на рис. 2.
|
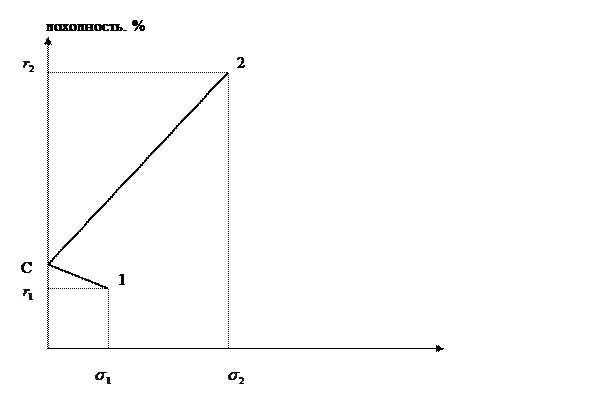
Рис. 2 График зависимости доходности портфеля от го риска при коэффициенте корреляции = -1.
На данном рисунке точка С – безрисковый портфель (в таком случае риск портфеля равен 0). В таком случае 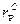 - доходность безрискового портфеля.
- доходность безрискового портфеля.
В данном случае возникает понятие доминирующего портфеля. Доминирующий портфель – это портфель, обеспечивающий более высокую доходность при одинаковом уровне риска.
В нашем случае это линия С-2.
Чтобы определить удельные веса данных активов в доминирующем портфеле мы должны решить следующую систему:
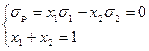
 (16)
(16)
 (17)
(17)
· Если коэффициент корреляции равен 0, то между инвестициями не существует никакой зависимости. В этом случае формула становится следующей:

График зависимости доходности портфеля от его риска следующий:

Рис. 3 График зависимости доходности портфеля от го риска при коэффициенте корреляции = 0.
Точка Д – портфель с минимальным риском.
Линия Д-2 – линия доминирующих портфелей.
Задание.Найти  и
и  в точке Д.
в точке Д.
ответ 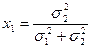 (18)
(18)
и 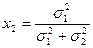 (19)
(19)
· Если значение коэффициента корреляции находится в пределах (-1;0) и (0;+1).
В этом случае подставляем конкретное коэффициента корреляции в формулу определения риска портфеля и находим конкретное значение риска данного портфеля.
График зависимости доходности от риска.
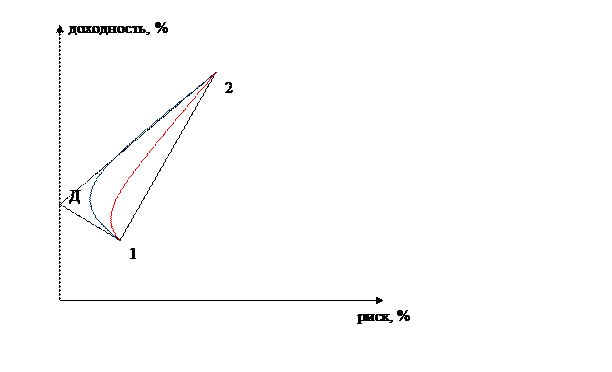
График зависимости доходности портфеля от риска лежит в пределах этого треугольника.
В данном случае также существует портфель с минимальным риском. Для нахождения удельных весов активов нужно взять производную из формулы ($),приравнять ее к нулю и найти веса.
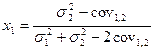 (20)
(20)
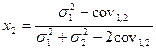 (21)
(21)
Дата добавления: 2015-11-10; просмотров: 1125;