Теплопроводность при нестационарном состоянии
Основные решения. Как отмечалось выше, при нестационарном состоянии с течением времени происходит изменение температуры тела, т. е. дТ/дt ¹ 0.
Подобное изменение температуры тела возможно, когда тело остывает или когда оно нагревается. На практике это широко распространенный процесс нагрева металла. Решение дифференциального уравнения теплопроводности совместно с краевыми условиями представляет собой весьма сложную математическую задачу, поэтому остановимся лишь на решении при краевых условиях III рода, получившем наибольшее практическое распространение. На практике часто встречаются печи, в которых нагрев металла происходит при неизменной температуре рабочего пространства. Некоторые печи с изменяющейся температурой по длине печи можно условно разделить на расчетные участки с приближенно неизменной температурой в пределах каждого участка и к каждому из них применить решения, полученные при краевых условиях III рода.
Приведем без вывода окончательное решение дифференциального уравнения теплопроводности для бесконечной плиты при краевых условиях III рода, которое имеет следующий вид:
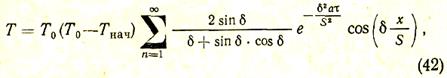
где Т0— температура печи (среды), К; Тнач — температура металла в начальный момент нагрева, К; а — коэффициент температуропроводности, м2/с; t — время нагрева (или охлаждения) тела, с; S — расчетная толщина нагреваемого тела, м; d — величина, зависящая от aS/l; a — коэффициент теплоотдачи (от газа к металлу), Вт/(м2×К); х — расстояние от центра тела до той точки, для которой определяют температуру Т, м.
 Анализируя уравнение (42), можно видеть, что температура нагрева металла Т зависит от трех безразмерных комплексов: критериев аt/S2, aS/l и х/S и что уравнение (42) может быть заменено критериальным уравнением следующего вида:
Анализируя уравнение (42), можно видеть, что температура нагрева металла Т зависит от трех безразмерных комплексов: критериев аt/S2, aS/l и х/S и что уравнение (42) может быть заменено критериальным уравнением следующего вида:
(43)
где q — безразмерный температурный критерий; Т0 — температура среды (печи); Тнач и Ткон —температура нагреваемого тела соответственно начальная и конечная.
В зависимости от условий решения уравнения Тконможет представлять собой как конечную температуру поверхности тела (при х/S = 1), так и конечную температуру в центре тела (при х/S = 0).
Безразмерный комплекс аt/S2 представляет собой известный критерий Фурье, а безразмерный комплекс aS/l — критерий Био.
Безразмерный геометрический симплекс х/S определяет собой местоположение точки в теле, для которой определяют температуру. Так, для центра нагреваемого тела x = 0 и х/S = 0, для поверхности тела x = S и х/S = 1.
Таким образом, решая уравнение (43) для поверхности тела (х/S = 1), получаем температурный критерий
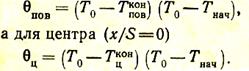
Характер нагрева тел существенно зависит от критерия Вi. Данное решение (42) целесообразно использовать при Вi>0,5.
Аналогичные решения уравнения (42) могут быть получены с краевыми условиями I и II рода, расчеты по которым рассмотрены во II томе данного учебника. Для инженерных расчетов зависимости типа (43) обычно представляются в графическом виде.
В металлургии и машиностроении распространенным процессом нестационарной теплопроводности является процесс нагрева металла перед обработкой давлением и для термической обработки. В процессе нагрева изменяется не только температура металла, но и его физические свойства (l, с, r) и коэффициент теплоотдачи. Однако аналитические решения типа (42) и (43) получены при условии, что эти величины не изменяются во времени. Поэтому для получения надежных результатов весь период нагрева целесообразно разбивать на интервалы и в пределах каждого интервала температуру усреднять и по ней выбирать и определять l, с, r и a.
Метод конечных разностей. Некоторые практические задачи могут быть решены с применением приближенных методов. К их числу относится метод конечных разностей (метод Шмидта), который часто применяют для нагрева или остывания огнеупорной футеровки печи. Этот метод основан на том, что в дифференциальном уравнении теплопроводности бесконечно малые величины заменяют малыми, но уже конечными величинами. Дифференциальное уравнение теплопроводности для одномерного потока имеет вид
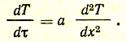
Если бесконечно малые приращения dТ, dt, dх заменить конечными малыми прираш.ениями, то уравнение можно записать так:
 (44)
(44)
В этом уравнении конечные малые приращения представляют собой: Dt — отрезок времени, в течение которого происходит изменение температуры DT, с; Dx — толщину элементарного слоя нагреваемого материала, на протяжении которой происходит изменение температуры в течение времени Dt, м.
Для практического применения этого метода необходимо выбрать значения величин Dx и Dt
Для определения Dx всю стенку конечной толщины следует произвольно разделить на некоторое число равных по толщине слоев и таким образом определить величину Dx, выраженную в метрах, а следовательно, и число слоев m = x/Dx. Отсчет слоев Dx следует вести от более нагретой стороны стенки к менее нагретой: Dx1 — слой, расположенный непосредственно у более нагретой поверхности, а Dxm — слой, расположенный около холодной поверхности.
Отрезок времени Dt определяют в зависимости от величины по выражению
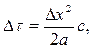
где а — коэффициент температуропроводности, м2/с.
Задача расчета заключается в том, чтобы установить распределение температур в стенке по истечении определенного времени t, прошедшего с момента начала нагрева. Таким образом, частное n = t/Dt дает число расчетных отрезков времени, из которых Dt1 — начальный, а Dtк — конечный отрезок времени, ч.
В начале нагрева, т. е. в начале отрезка, характеризующего время Dt1 температура нагреваемого тела в пределах каждого отрезка Dx считается неизменной. Обычно нагрев подобного рода происходит с одной стороны, поэтому для расчета необходимо знать температуру поверхности или закон изменения температуры поверхности с более нагретой стороны. Как более нагретой, так и менее нагретой поверхности стенки приписывается роль отдельных очень тонких слоев. Так, индекс Dx0 обозначает более нагретую поверхность, прилегающую к слою Dx1. Индекс Dxm+1 обозначает менее нагретую поверхность.
Методом конечных разностей наиболее часто пользуются для расчета прогрева стен в печах периодического действия, где зачастую представляется возможным задать изменение температуры поверхности стен с внутренней стороны, поскольку температура собственно поверхности бывает близка к температуре раскаленных газов, заполняющих печь. Однако температуру поверхности можно определить и расчетным путем по выражению
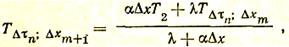 (45)
(45)
где 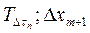 — температура поверхности Dxm+1 в любой отрезок времени, К; Т2— температура газовой среды, омывающей стенку, К; a — коэффициент теплоотдачи от стенки к газу, Вт/(м2×К); l — коэффициент теплопроводности материала стенки, Вт/(м×К).
— температура поверхности Dxm+1 в любой отрезок времени, К; Т2— температура газовой среды, омывающей стенку, К; a — коэффициент теплоотдачи от стенки к газу, Вт/(м2×К); l — коэффициент теплопроводности материала стенки, Вт/(м×К).
Температура в каждом слое стенки в определенный отрезок времени может быть определена как полусумма температур предыдущего и последующего слоев в предшествующий отрезок времени. Так
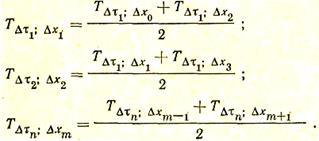
Таким образом, можно получить распределение температур в плоской однородной стенке. Однако если стенка состоит из двух различных материалов (например, шамот + тепловая изоляция), то в расчет необходимо внести некоторые дополнения. Первую стенку х,как и в случае однородной стенки, следует разделить на определенное число элементарных слоев Dx, причем отрезки времени должны быть получены из уравнения

Эти отрезки времени должны быть, естественно, одинаковыми для первой и второй стенок, т. е. Dtx = Dty =Dt.
Поэтому толщину элементарных слоев второй стенки у нельзя выбирать произвольно; ее следует определять по выражению
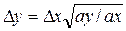 ,
,
где ах и аy — коэффициенты температуропроводности первой и второй стенок, м2/с.
В пределах каждой из двух стенок температуру элементарных слоев определяют, как и для однородной стенки. Температуру поверхности также определяют по выражению (45).
В месте соприкосновения двух материалов температуру можно найти по выражению
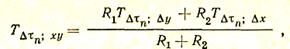 (46)
(46)
где 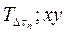 — температура в месте соприкосновения двух стенок в произвольный отрезок времени Dtn, К;
— температура в месте соприкосновения двух стенок в произвольный отрезок времени Dtn, К; 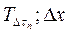 и
и 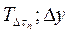 — температура соприкасающихся слоев соответственно первой и второй стенок в тот же отрезок времени Dtn, К; R1 = Dx/l1 и R2 = Dx/l2 — тепловое сопротивление элементарных слоев первой и второй стенок.
— температура соприкасающихся слоев соответственно первой и второй стенок в тот же отрезок времени Dtn, К; R1 = Dx/l1 и R2 = Dx/l2 — тепловое сопротивление элементарных слоев первой и второй стенок.
Выяснив таким образом, каково распределение температур, можно путем простого арифметического усреднения получить среднюю температуру прогретой стенки и определить то количество тепла, которое аккумулировано стенкой в процессе нагрева. Аккумулирование тепла кладкой является очень важной расходной статьей теплового баланса периодически действующих печей.
Дата добавления: 2015-11-10; просмотров: 2041;
