Теплопроводность при стационарном состоянии

При стационарном тепловом состоянии температура с тече­нием времени остается неизменной. В практике металлурги­ческой теплотехники подобные случаи передачи тепла теплопроводностью встречаются при передаче тепла через плоские стенки.

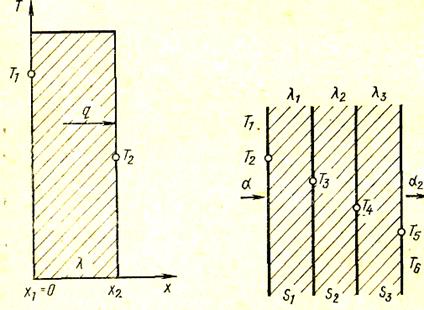
Рис. 27. Плоская однослой- Рис. 28. Плоская трехслойная

ная стенка стенка

Однослойная стенка. Чтобы получить выражения, позво­ляющие определить распределение температур в стенке и количество передающегося через нее тепла, необходимо ре­шить дифференциальные уравнения теплопроводности со­вместно с краевыми условиями I рода. Применительно к этому случаю (рис. 27), когда тепло передается через стенку толщиной s = х₂— x₁ от поверхности с температурой Т₁к поверхности с температурой Т₂, изменение температу­ры по толщине стенки описывается уравнением

(40)

а плотность теплового потока, проходящего через стенку, Вт/м²

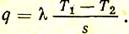
Следует заметить, что выражение (40) представляет собой уравнение прямой линии, следовательно, распростра­нение температуры в однослойной плоской стенке при l = const имеет прямолинейный характер. Если l, зависит от температуры, то распределение температуры имеет криво­линейный характер, причем кривая выгибается вверх, когда l увеличивается с повышением температуры, и вниз, когда l, уменьшается с увеличением температуры.

Многослойная стенка. Рассмотрим плоскую стенку, со­стоящую из трех слоев (рис. 28). Можно принять любое число слоев, причем каждый из них может обладать свои­ми физическими свойствами. Чтобы получить выражение, позволяющее определить количество тепла, проходящее через многослойную стенку, необходимо помнить, что для стационарного процесса плотность теплового потока, про­ходящего через каждый слой, одинакова, т. е. q₁ = q₂ = q₃ = q

Как видно, знаменатель данного уравнения представля­ет собой сумму тепловых сопротивлений отдельных слоев.

Передача тепла от более нагретого газа к менее нагре­тому через плоскую стенку. На практике часто приходится определять количество тепла, которое требуется передать от одного газа к другому (или к жидкости) через стенку (многослойную или однослойную), т. е. решать задачу, по­добную изображенной на рис. 28.

Поскольку рассматривается стационарное тепловое со­стояние, постольку температуры теплоотдающего газа Т₁и тепловоспринимающего газа Т₆,так же как и величины Т₂, Т₃, Т₄, и Т₅ остаются во времени неизменными. Соблюдение постоянства температуры окружающей среды — есть усло­вие, присущее граничным условиям III рода. Процесс теп­лообмена определяется в данном случае коэффициентами теплоотдачи a₁ и a₂.

Плотность теплового потока, который отдается более нагретым газом, может быть определена по выражению

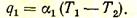
Плотность теплового потока, который передается через стенку, была определена в предыдущем разделе:

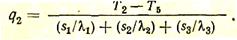
Плотность теплового потока, передаваемого от стенки к менее нагретому газу:

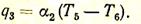
При стационарном состоянии

После сложения этих трех уравнений, получаем

(41)

Как указывалось выше, величина обратная коэффициен­ту теплоотдачи 1/a₁(или s/l), выражает тепловое сопро­тивление. Следовательно, знаменатель уравнения (41) представляет собой сумму тепловых сопротивлений различ­ных звеньев передачи тепла. Уравнение (41) может быть записано в виде:

q = K(T₁ – T₆),

Величину К называют коэффициентом теплопередачи. Напомним, что разница между терминами «теплоотдача» и «теплопередача» заключается в том, что термин теплоотда­ча применим для какой-либо одной ступени передачи тепла, например от газа к стенке, от стенки к газу и т. п. Термин «теплопередача» применим для обозначения более сложно­го процесса передачи тепла, включающего в себя несколько ступеней этого процесса, например передачу тепла от газа к газу через стенку, где наблюдаются три ступени теплоперехода: от газа к стенке, через стенку и от стенки к друго­му газу. Подобным же образом можно объяснить различие между коэффициентом теплоотдачи a и коэффициентом теплопередачи K.