Свободная конвекция
Обычно, говоря о свободной конвекции, различают два вида этого процесса в зависимости от его протекания в неограниченном или ограниченном пространстве. Различие между этими процессами заключается в следующем. Представим себе, что две поверхности участвуют в теплообмене: одна отдает тепло воздуху, т. е. происходит процесс нагрева воздуха, а другая, наоборот, отбирает тепло от подогретого воздуха и тем самым его охлаждает. Если обе поверхности значительно удалены одна от другой, то оба процесса (нагрев и охлаждение воздуха) происходят, не влияя друг на друга. В этом случае можно говорить о свободной конвекции в неограниченном пространстве. Понятно, что, если протекает практически только один процесс (нагрев или охлаждение), то наблюдается теплоотдача в неограниченном пространстве. Если пространство ограничено, то процессы нагрева и охлаждения разделить невозможно и все явления надо рассматривать в целом.
Свободная конвекция в неограниченном пространстве. Типичным свободным движением в неограниченном пространстве для вертикальной нагретой поверхности является такое движение, когда около нижней части поверхности происходит ламинарное движение, а в верхней части —турбулентное. Вид движения зависит от разности температур стенки и воздуха. С изменением вида движения изменяется и вид теплоотдачи. Можно показать, что в нижней части толщина ламинарного слоя сначала увеличивается и коэффициент теплоотдачи уменьшается, а затем происходит стабилизация турбулентного движения и коэффициент теплоотдачи остается неизменным.
Свободная конвекция в неограниченном пространстве для тел самой различной формы в настоящее время хорошо изучена. Проведенная обработка результатов многочисленных исследований позволила сделать следующие выводы:
1) форма тела имеет второстепенное значение; режим движения определяется не формой тела, а температурными условиями;
2) при определенных условиях процесс теплообмена не зависит от геометрических размеров и его можно изучить на малых моделях;
3) для процесса теплоотдачи определяющим критерием является произведение GrPr. Зависимость между критериями подобия Nu, Gr и Pr может быть представлена в виде:
Nu =C(GrPr)n,
где С и n— опытные коэффициенты, значения которых следующие:
| GrPr | 1×10-3 – 5×10-2 | 5×10-2 – 2×107 | 2×107 – 1×1013 |
| C | 1,18 | 0,54 | 0,135 |
| n | 1/8 | 1/4 | 1/3 |
Свободная конвекция в ограниченном, пространстве. Поскольку для теплоотдачи в ограниченном пространстве нельзя получить верные коэффициенты теплоотдачи, постольку для облегчения расчета такой сложный процесс теплообмена рассматривают как элементарное явление передачи тепла теплопроводностью, вводя при этом понятие эквивалентного коэффициента теплопроводности lэк.Это позволяет избежать определения коэффициентов теплоотдачи a. Значение lэк находят опытным путем.
Если эквивалентный коэффициент теплопроводности разделить на действительный коэффициент теплопроводности той же среды при ее средней температуре, то получаем новый коэффициент, который характеризует влияние конвекции и называется коэффициентом конвекции eк = lэк/l.
Коэффициент eк является функцией произведения GrPr, т. е. eк = f(GrPr).
В подобной форме обрабатывают опытные данные для свободной конвекции в ограниченном пространстве.
При значениях произведения GrPr<1000 величина eк = 1. При значениях GrPr>1000 может быть использовано уравнение
eк = 0,18(GrPr)0,25.
Получив значение lэк, нетрудно определить плотность теплового потока по уравнению Фурье, Вт/м2
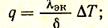
где d — толщина слоя, участвующего в теплообмене, м; DТ — разность температур на границах слоя, К.
Дата добавления: 2015-11-10; просмотров: 4653;
