Применение теории подобия к изучению теплообмена

Так же, как и при гидродинамическом подобии, услови­ем теплового подобия является равенство соответствующих инвариантов или критериев подобия.

Как показывает теория, для достижения теплового подо­бия при вынужденном движении необходимо равенство сле­дующих критериев подобия двух явлений:

Фурье

Fо = Fо' или at/l = a't'/l';

Пекле

Fе = Fе' или wl/а = w'l'/а';

Нуссельта

Nu = Nu' или al/l = a'l'/l',

где w — скорость движения среды (жидкости или газа), м/с; l — характерный геометрический размер, м; t — время, с (ч); l — коэффициент теплопроводности, Вт/(м×К); а — коэффициент температуропроводности, м²/с; a — коэффи­циент теплоотдачи, Вт/(м²×К).

На практике часто производят различные преобразова­ния с критериями. Так, критерий Пекле может быть запи­сан следующим образом:

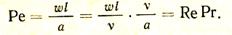
Отношение v/а = Рr представляет собой критерий Прандтля.

Все критерии имеют определенный физический смысл, в соответствии с которым они применяются.

Критерий Фурье часто называют безразмерным време­нем, поскольку в числителе этого критерия стоит время т. В стационарных процессах критерий Fо опускается. Выше отмечалось, что коэффициент температуропроводности а характеризует интенсивность изменения энтальпии тела, т. е. интенсивность его нагрева или охлаждения. Таким образом, в целом критерий Фурье характеризует связь между скоро­стью изменения температуры тела, его физическими характеристиками и размерами.

Физический смысл критерия Пекле становится ясным, если написать его несколько иначе:

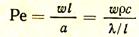
При этом числитель представляет собой плотность (на единицу площади сечения) теплового потока, переносимого движущейся средой, а знаменатель — плотность теплового потока теплопроводностью. Поэтому критерий Пекле является показателем соотношения переноса тепла конвекцией и теплопроводностью.

Критерий Прандтля (Pr = v/а = vrc/l) является мерой подобия температурных и скоростных полей. Ниже будет показано, что между процессами теплопередачи и гидроди­намики существует (в определенных условиях) подобие. При Pr = 1 поля температур и скоростей подобны.

Конвекция обязательно связана с движением, которое, как выше отмечалось, может быть вынужденным и свобод­ным.

Критерий Rе характеризует вынужденное движение:

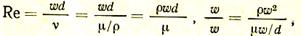
так как представляет собой отношение инерционных сил (rw²) к силам трения (mw/d).

Для свободного движения применяется критерий Грасгофа:

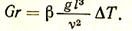
Свободное движение возникает как результат разности плотностей, определяемой перепадом температур DT. В ре­зультате наличия разности температур DT создается раз­ность плотностей r — r₀, от которой зависит коэффициент объемного расширения b = (r — r₀)/r. Таким образом, кри­терий Gr характеризует меру отношения подъемной силы к силе вязкого трения при свободном движении.

Критерий Нуссельта ( 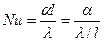) характеризует связь между интенсивностью теплоотдачи и температур­ным полем в пограничном слое.

Следует отметить, что при нагреве различных материа­лов обычно различают так называемые внешнюю и внут­реннюю задачи.

Внешняя задача рассматривает передачу тепла от эле­ментов печи к поверхности материалов. Внешнюю задачу характеризует критерий Нуссельта, в котором l — коэффици­ент теплопроводности газа (жидкости).

Внутренняя задача рассматривает передачу тепла от по­верхности материала внутрь. В этом случае применяется критерий Био (Вi = al/l), внешне похожий на критерий Nu. Но в критерии Био l означает теплопроводность мате­риала, а l — его толщину.

Чаще всего целью экспериментального изучения кон­вективного теплообмена является определение коэффициен­та теплоотдачи a. Поэтому опытные данные обычно обра­батывают в виде критериального уравнения

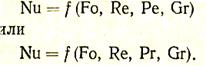(39)

Для ряда конкретных задач это общее критериальное уравнение упрощается. Например, при стационарном состо­янии выпадает критерий Fо:

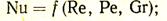
при стационарном вынужденном движении, кроме крите­рия Fо, выпадает также критерий Gr:

Nu = f(Re, Pr).

Наоборот, при свободном стационарном движении выпа­дают Fо и Rе:

Nu = f(Pr, Gr).

Для газов с молекулой, состоящей из четырех и более атомов, Pr = 1 и для вынужденного стационарного движе­ния Nu = f(Rе), а для свободного стационарного движения Nu = f(Gr).