Теплообмен излучением между серыми поверхностями, разделенными лучепрозрачной средой
Угловые коэффициенты. На практике часто приходится решать задачу о том, какая доля тепла, излучаемого источником, попадает на ту или иную поверхность. Для решения таких задач пользуются понятием углового коэффициента или коэффициента облученности.
 Для примера рассмотрим электрическую печь, поперечный профиль которой изображен на рис. 30. Электрические нагревательные элементы расположены на своде излучающем тепловой поток Q во всех направлениях. Предположим, что свод плоский (подвесной конструкции). Допустим, свод излучает Q1и Q2соответственно на левую и правую боковую стенки и Q3 на лежащий на полу металл. Таким образом, на левую стенку свод излучает часть тепла, равную Q1/Q, на правую Q2/Q и на металл Q3/Q. Каждое из этих отношений называют угловым коэффициентом, который обычно обозначают буквой j. Если обозначить свод индексом 4, то отношение Q1/Q = j4,1 представляет собой угловой коэффициент от поверхности свода на левую стену. Соответственно Q3/Q = j4,3 — угловой коэффициент излучения от свода на металл и т. д. Таким образом, угловой коэффициент показывает, какая часть всей излучаемой тепловой энергии одного тела (поверхности) попадает на другое тело (другую поверхность).
Для примера рассмотрим электрическую печь, поперечный профиль которой изображен на рис. 30. Электрические нагревательные элементы расположены на своде излучающем тепловой поток Q во всех направлениях. Предположим, что свод плоский (подвесной конструкции). Допустим, свод излучает Q1и Q2соответственно на левую и правую боковую стенки и Q3 на лежащий на полу металл. Таким образом, на левую стенку свод излучает часть тепла, равную Q1/Q, на правую Q2/Q и на металл Q3/Q. Каждое из этих отношений называют угловым коэффициентом, который обычно обозначают буквой j. Если обозначить свод индексом 4, то отношение Q1/Q = j4,1 представляет собой угловой коэффициент от поверхности свода на левую стену. Соответственно Q3/Q = j4,3 — угловой коэффициент излучения от свода на металл и т. д. Таким образом, угловой коэффициент показывает, какая часть всей излучаемой тепловой энергии одного тела (поверхности) попадает на другое тело (другую поверхность).
Угловые коэффициенты связаны между собой определенными соотношениями. Рассмотрим основные из них.
1. Правило замыкаемости. Очевидно, что для замкнутой системы (рис. 30, а)
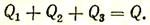
Разделив все члены этого уравнения на Q, получаем
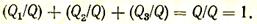
Однако Q1/Q = j4,1 и т.д., следовательно:
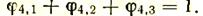
Таким образом, сумма угловых коэффициентов для замкнутой системы равна единице, т. е. Sj = 1. Понятно, что никакое значение любого углового коэффициента никогда не может быть больше единицы. Действительно, не может же сумма Q1 + Q2 + Q3 быть больше Q.
2. Правило взаимности. Установлено, что если две поверхности F1и F2излучают друг на друга, то будет справедливо равенство
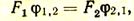
где j1,2 — угловой коэффициент с поверхности 1 на поверхность 2; j2,1 — то же, с поверхности 2 на поверхность 1.
Необходимо отметить, что возможны и такие случаи, когда лучистым теплом обмениваются элементы одной и той же поверхности. Если в приведенном выше примере свод был бы не плоским, а вогнутым (арочным), то наряду с излучением на другие поверхности свод излучал бы «сам на себя» (рис. 30,6). В этом случае применимо другое уравнение:
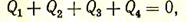
где Q4 — тепловой поток, излучаемый всеми элементами поверхности свода друг на друга.
Соответственно угловой коэффициент j4,4, представляющий собой отношение Q4/Q, также может быть назван угловым коэффициентом тела, излучающего само на себя.
Если в теплообмене излучением участвует вогнутая поверхность, правило замыкаемости следует писать обязательно с учетом углового коэффициента излучения само на себя, т.е. для нашего примера это правило можно записать следующим образом:
j4,1 + j4,2 + j4,3 + j4,4 = 1.
Угловой коэффициент j4,4 для плоского и выпуклого тел равен нулю.
Рассмотрим несколько примеров определения угловых коэффициентов (рис. 31), имеющих определенное практическое значение. Так, пример, показанный на рис. 31, a, достаточно точно соответствует соотношению для нагревательной печи с плоским подвесным сводом. Пример на рис. 31,б представляет собой некоторое подобие взаимного расположения факела (поверхность F1) и обмуровки печи. Пример на рис. 31, в также представляет собой некоторое подобие взаимного расположения футеровки печи (F2)и поверхности металлической ванны в мартеновской или двухванной печи.
Для этих примеров угловые коэффициенты имеют следующие выражения:
1. Две большие, близко расположенные друг к другу плоскости. Используя правило замыкаемости, можно написать j1,1 + j1,2 = 1 и j2,2 + j2,1 = 1; но если для плоскости j1,1 = 0 и j2,2 = 0, то j1,2 = j2,1 = 1.
2. Две концентрические шаровые поверхности или два одноосных длинных цилиндра. По правилу замыкаемости j1,1 + j1,2 = 1 и j2,2 + j2,1 = 1. Но j1,1 = 0, следовательно, j1,2 = 1.
Отсюда, по правилу взаимности F1j1,2 = j2,1F2, можно получить, что j2,1 = F1/ F2и, наконец, j2,2 = 1—( F1/ F2).
3. Внутренняя поверхность F2сегмента длинного цилиндра и плоскость F1, являющаяся основанием сегмента.

Рис. 31. Замкнутые системы из двух тел
Этот случай представляет собой некоторое подобие взаимного положения внутренней обмуровки печи и металла, заполняющего под печи. Повторив выкладки, приведенные для 2-го примера, получаем
j1,2 = 1; j2,1 = F1/ F2; j2,2 = 1—( F1/ F2).
Угловыми коэффициентами, найденными расчетом, пользуются для решения практических задач.
Теплообмен излучением между серыми поверхностями, образующими замкнутую систему. Теплообмен между серыми поверхностями, образующими замкнутую систему, часто встречается на практике, причем теплообмен между серыми поверхностями, степень черноты которых меньше единицы, включает не только прямые потоки, но и отраженные. Если в состоянии теплообмена находится несколько серых поверхностей, то расчет значительно затруднен. Поэтому выведем общую формулу лучистого теплообмена только между двумя серыми поверхностями, воспользовавшись для этого методом сальдо-потока, разработанным советским ученым Г.Л. Поляком. Прежде всего уточним смысл некоторых терминов, для чего рассмотрим поверхность F, представленную на рис. 32, с температурой Т и степенью черноты e.
Рассмотрим, как происходит теплообмен у этой поверхности. К поверхности поступает падающий тепловой поток Qпад. Часть его поглощается поверхностью F и, следовательно, поглощенный поток Qпогл = Qпадe. Другая его часть отражается, и, следовательно, отраженный поток
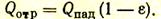
Поскольку тело нагрето (T>0), оно излучает собственные лучи, образующие тепловой поток собственного излучения
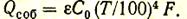
 Сумма собственного излучения и отраженных потоков составляет эффективное излучение, т. е.
Сумма собственного излучения и отраженных потоков составляет эффективное излучение, т. е.
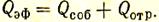
Тело не только поглощает тепло Qпогл, но и отдает тепло в виде собственного излучения Qсоб. Поэтому можно говорить о результирующем тепловом потоке, или, иначе, о сальдо-потоке:
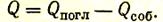 (52)
(52)
Если Qпогл > Qсоб, то сальдо-поток имеет положительное значение; если Qпогл < Qсоб, то Q имеет отрицательное значение. Найдем связь между сальдо-потоком Q и эффективным излучением. Используем приведенное выше выражение (52). Учтя, что
Qпогл = Qпад – Qотр и Qсоб = Qэф – Qотр,
и подставив выражения для Qпогл и Qсоб в уравнение (53), получаем
Q = Qпад – Qотр – Qэф + Qотр = Qпад – Qэф (52')
или Qэф = Qпад – Q.
Однако Qпад = Qпогл/e и тогда Qэф = (Qпогл/e) – Q.
По уровнению (52) Qпогл = Q + Qсоб. Следовательно:
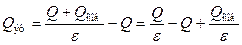
и окончательно
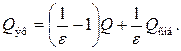 (53)
(53)
Выражение (53) необходимо для дальнейших выкладок с целью получения расчетной формулы.
Так как мы выводим формулу для теплообмена излучением между двумя серыми замкнутыми поверхностями, прежде всего установим, какое количество тепла первое тело излучает на второе. Если эффективный поток от поверхности первого тела обозначим через Q1,эф, то на второе тело будет падать часть этого потока, определяемая величиной углового коэффициента с тела первого на тело второе (j1,2), т.е. падающий тепловой поток на второе тело
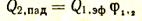
Аналогично этому можно написать, что падающий тепловой поток на первое тело
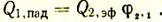
Если Т2>Т1, то количество тепла, которое первое тело будет получать от второго, соответствует сальдо-потоку Q1 равному разности падающих тепловых потоков, т.е.
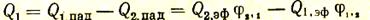
Подставим в это выражение значение эффективных тепловых потоков по уравнению (53):
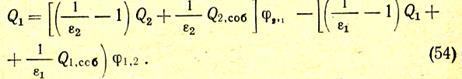
Но если рассматривается теплообмен между двумя телами в замкнутой системе, то сколько тепла отдаст второе тело, столько первое получит, т. е. Q1 = — Q2.
Заменив теперь в выражении (54) Q2 на —Q1 получаем одно уравнение с одним неизвестным Q1 которое и решим относительно этого неизвестного:
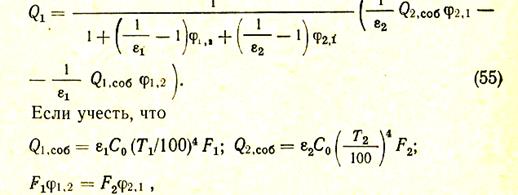
| а 2\ — |
и подставить соответствующие выражения в уравнение (55), то получим
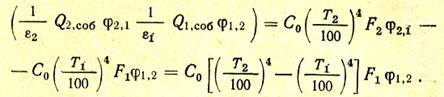
Следовательно, выражение для определения Q можно представить в виде
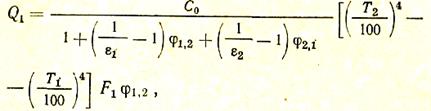
или
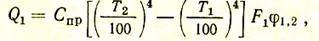
где Спр — приведенный коэффициент излучения, определяемый по уравнению
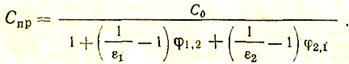 (56)
(56)
С использованием выражения (56) можно получить значения приведенных коэффициентов для конкретных случаев, рассмотренных в предыдущем разделе.
Так, для двух близко расположенных бесконечных плоскостей (пример 1, j1,2 = j2,1 = 1)
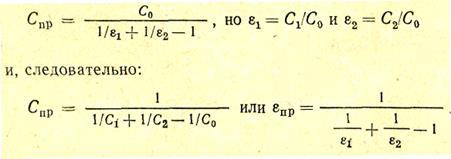
Для примеров 2 и 3, когда j1,2 = 1, а j2,1 = F1/F2, приведенный коэффициент излучения
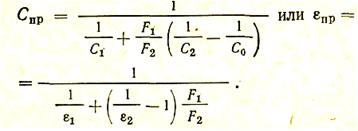
Рассмотренный метод расчета применим для решения ряда технических задач теплообмена излучением в замкнутом пространстве (например, печи) между двумя телами.
 Защита от излучения с помощью экранов. Для того чтобы ослабить лучистый поток, падающий на обслуживающий печь персонал, применяют тепловые экраны, выполняемые обычно из тонкого стального листа.
Защита от излучения с помощью экранов. Для того чтобы ослабить лучистый поток, падающий на обслуживающий печь персонал, применяют тепловые экраны, выполняемые обычно из тонкого стального листа.
Предположим, что температура какой-либо тепло-излучающей поверхности равна Т. Рядом с этой поверхностью помещен тонкий экран (рис.33).
Поверхность металлической обмуровки печи и поверхность экрана обычно весьма окислены, и поэтому их можно считать абсолютно черными, и тогда С=Сэ=С0. Площадь излучающей поверхности и площадь экрана равна F. Определим, насколько уменьшится тепловой поток излучением в результате применения экрана. Найдем прежде всего температуру экрана Тэ. Для двух близко расположенных плоскостей применима формула
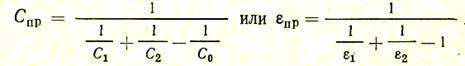
Так как в нашем случае С1 = С2 = С0, то Спр = С0. Следовательно, тепловой поток, который получит экран от излучающей поверхности, равен, Вт
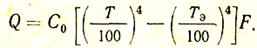
Но экран будет излучать в атмосферу цеха тепловой поток
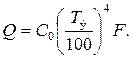
Приравняем эти два выражения
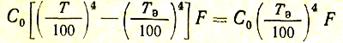
и из этого равенства найдем, что
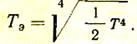
Используя полученное выражение для Тэ, можно определить тепловой поток, излучаемый экраном в атмосферу цеха
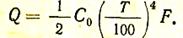
Поскольку поверхность без экрана излучает тепловой поток Q1, равный
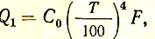
то можно сделать вывод, что применение экрана уменьшило лучистый тепловой поток в два раза, т. е.
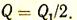
Если установлено п экранов, то, рассуждая аналогичным путем, можно показать, что
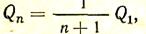
где Qn — тепловой поток, передаваемый излучением при наличии экранов; Q1— тепловой поток без экранов.
Если поверхность экранов не является черной, то приведенный коэффициент eпр для числа экранов, равного п, может быть определен из выражения
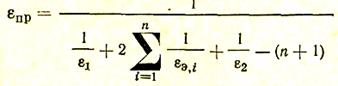
где eэ,і — степень черноты каждого экрана.
Дата добавления: 2015-11-10; просмотров: 2884;
